Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1989.
Hypergraphs - Combinatorics of Finite Sets.
Vol. 45,
Issue. ,
p.
237.
Hedetniemi, S.T.
and
Laskar, R.C.
1990.
Bibliography on domination in graphs and some basic definitions of domination parameters.
Discrete Mathematics,
Vol. 86,
Issue. 1-3,
p.
257.
Hedetniemi, S.T.
and
Laskar, R.C.
1991.
Topics on Domination.
Vol. 48,
Issue. ,
p.
257.
Dourado, Mitre C.
Protti, Fábio
and
Szwarcfiter, Jayme L.
2006.
Computational aspects of the Helly property: a survey.
Journal of the Brazilian Computer Society,
Vol. 12,
Issue. 1,
p.
7.
Barthélemy, Jean-Pierre
Gusho, Gentian
and
Osswald, Christophe
2007.
Selected Contributions in Data Analysis and Classification.
p.
137.
De Caria, Pablo
and
Gutierrez, Marisa
2012.
On minimal vertex separators of dually chordal graphs: Properties and characterizations.
Discrete Applied Mathematics,
Vol. 160,
Issue. 18,
p.
2627.
Bretto, Alain
2013.
Hypergraph Theory.
p.
111.
Bretto, Alain
2013.
Hypergraph Theory.
p.
23.
Torres, Luis M.
and
Wagler, Annegret K.
2013.
Analyzing the dynamics of deterministic systems from a hypergraph theoretical point of view.
RAIRO - Operations Research,
Vol. 47,
Issue. 3,
p.
321.
Ali Balcı, Mehmet
and
Akgüller, Ömer
2014.
Average Weakly Hyperedge Domination Number for a Hypergraph and Actor-Network Application.
International Journal of Modeling and Optimization,
Vol. 4,
Issue. 5,
p.
346.
Guttmann-Beck, Nili
Rozen, Roni
and
Stern, Michal
2021.
Vertices removal for feasibility of clustered spanning trees.
Discrete Applied Mathematics,
Vol. 296,
Issue. ,
p.
68.
Zhang, Xin
Ni, Qin
Sheng, Zhou
and
Ge, Zhili
2021.
Computing the largest H-eigenvalue of large-scale tensors generated from directed hypergraphs.
Computational and Applied Mathematics,
Vol. 40,
Issue. 5,
Hamzekolaee, Ali Reza Moniri
and
Norouzi, Morteza
2023.
Applying a hypergraph to determine the structure of some finite modules.
Journal of Applied Mathematics and Computing,
Vol. 69,
Issue. 1,
p.
675.
Guttmann-Beck, Nili
and
Stern, Michal
2024.
Decomposing the feasibility of Clustered Spanning Tree by Paths.
Discrete Applied Mathematics,
Vol. 354,
Issue. ,
p.
160.
Abbas, Muntaha Khudhair
and
Hamzekolaee, Ali Reza Moniri
2025.
A hypergraph on modules and singularity condition.
Discrete Mathematics, Algorithms and Applications,
Vol. 17,
Issue. 06,

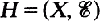 is a subtree of a tree (SOFT) hypergraph if there exists a tree T such that X=V(T) and for each
is a subtree of a tree (SOFT) hypergraph if there exists a tree T such that X=V(T) and for each 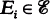 there is a subtree T
there is a subtree T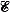 has the Helly property and
has the Helly property and 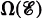 , the intersection graph of
, the intersection graph of 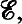 is chordal. Results of Berge and Gavril have previously shown these to be necessary conditions.
is chordal. Results of Berge and Gavril have previously shown these to be necessary conditions.