No CrossRef data available.
Article contents
Büchi’s Problem in Modular Arithmetic for Arbitrary Quadratic Polynomials
Part of:
Sequences and sets
Published online by Cambridge University Press: 26 April 2019
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Given a prime 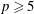 $p\geqslant 5$ and an integer
$p\geqslant 5$ and an integer 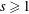 $s\geqslant 1$, we show that there exists an integer
$s\geqslant 1$, we show that there exists an integer 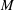 $M$ such that for any quadratic polynomial
$M$ such that for any quadratic polynomial 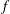 $f$ with coefficients in the ring of integers modulo
$f$ with coefficients in the ring of integers modulo 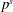 $p^{s}$, such that
$p^{s}$, such that 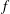 $f$ is not a square, if a sequence
$f$ is not a square, if a sequence 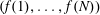 $(f(1),\ldots ,f(N))$ is a sequence of squares, then
$(f(1),\ldots ,f(N))$ is a sequence of squares, then 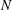 $N$ is at most
$N$ is at most 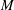 $M$. We also provide some explicit formulas for the optimal
$M$. We also provide some explicit formulas for the optimal 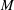 $M$.
$M$.
Keywords
MSC classification
Primary:
11B50: Sequences (mod $m$)
Secondary:
11B83: Special sequences and polynomials
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
All three authors were partially supported by the grants “Fondecyt research projects 1130134 and 1170315, Chile” to author X. V., from Conicyt. Author M. V. was partially supported by the government of the Russian Federation (grant 14.Z50.31.0030).
References
Allison, D.,
On square values of quadratics
. Math. Proc. Cambridge Philos. Soc.
99(1986), no. 3, 381–383. https://doi.org/10.1017/S030500410006432X
Google Scholar
An, T. T. H., Huang, H.-L., and Wang, J. T.-Z.,
Generalized Büchi’s problem for algebraic functions and meromorphic functions
. Math. Z.
273(2013), no. 1–2, 95–122. https://doi.org/10.1007/s00209-012-0997-9
Google Scholar
An, T. T. H. and Wang, J. T. Y.,
Hensley’s problem for complex and non-Archimedean meromorphic functions
. J. Math. Anal. Appl.
381(2011), no. 2, 661–677. https://doi.org/10.1016/j.jmaa.2011.03.025
Google Scholar
Bremner, A.,
On square values of quadratics
. Acta Arith.
108(2003), 95–111. https://doi.org/10.4064/aa108-2-1
Google Scholar
Browkin, J. and Brzeziński, J.,
On sequences of squares with constant second differences
. Canad. Math. Bull.
49‐4(2006), 481–491. https://doi.org/10.4153/CMB-2006-047-9
Google Scholar
Garcia-Fritz, N.,
Quadratic sequences of powers and Mohanty’s conjecture
. Int. J. Number Theory
14(2018), no. 2, 479–507. https://doi.org/10.1142/S1793042118500306
Google Scholar
González-Jiménez, E. and Xarles, X.,
On symmetric square values of quadratic polynomials
. Acta Arith.
149(2011), no. 2, 145–159. https://doi.org/10.4064/aa149-2-4
Google Scholar
Lipshitz, L.,
Quadratic forms, the five square problem, and diophantine equations
, The collected works of J. Richard Büchi, eds. MacLane, S. and Siefkes, Dirk, Springer, 1990, pp. 677–680.Google Scholar
Mazur, B.,
Questions of decidability and undecidability in number theory
. J. Symbolic Logic
59‐2(1994), 353–371. https://doi.org/10.2307/2275395
Google Scholar
Pasten, H.,
Büchi’s problem in any power for finite fields
. Acta Arith.
149‐1(2011), 57–63. https://doi.org/10.4064/aa149-1-4
Google Scholar
Pasten, H., Pheidas, T., and Vidaux, X.,
A survey on Büchi’s problem: new presentations and open problems
. Zapiski POMI
377(2010), 111–140. https://doi.org/10.1007/s10958-010-0181-x
Google Scholar
Pasten, H. and Wang, J. T.-Y.,
Extensions of Büchi’s higher powers problem to positive characteristic
. Int. Math. Res. Not. IMRN
2015
no. 11, 3263–3297.Google Scholar
Pheidas, T. and Vidaux, X.,
The analogue of Büchi’s problem for rational functions
. J. London Math. Soc.
74(2006), no. 3, 545–565. https://doi.org/10.1112/S0024610706023283
Google Scholar
Pheidas, T. and Vidaux, X.,
Corrigendum: The analogue of Büchi’s problem for rational functions
. J. London Math. Soc.
82(2010), 273–278. https://doi.org/10.1112/jlms/jdq002
Google Scholar
Sáez, P., Vidaux, X., and Vsemirnov, M.,
Optimal bounds for Büchi’s problem in modular arithmetic
. J. Number Theory
149(2015), 368–403. https://doi.org/10.1016/j.jnt.2014.10.008
Google Scholar
Shlapentokh, A. and Vidaux, X.,
The analogue of Büchi’s problem for function fields
. J. Algebra
330(2010), 482–506. https://doi.org/10.1016/j.jalgebra.2011.01.008
Google Scholar
Vojta, P.,
Diagonal quadratic forms and Hilbert’s Tenth Problem
. In:
Hilbert’s tenth problem: relations with arithmetic and algebraic geometry
, Contemp. Math., 270, American Mathematical Society, Providence, RI, 2000, pp. 261–274. https://doi.org/10.1090/conm/270/04378
Google Scholar

