Hostname: page-component-cb9f654ff-lqqdg Total loading time: 0 Render date: 2025-08-30T17:27:38.364Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundedness of the q-Mean-Square Operator on Vector-Valued Analytic Martingales

Published online by Cambridge University Press:  20 November 2018

Liu Peide ,
Eero Saksman  and
Hans-Olav Tylli
Liu Peide
Affiliation:
Department of Mathematics Wuhan University Wuhan, Hubei 430072 P. R. China, email: pdlin@whu.edu.cn
Eero Saksman
Affiliation:
University of Jyväskylä and University of Helsinki Department of Mathematics University of Helsinki P. O. Box 4, Yliopistonkatu 5 FIN-00014 Helsinki Finland, email: saksman@cc.helsinki.fi
Hans-Olav Tylli
Affiliation:
Department of Mathematics University of Helsinki P. O. Box 4, Yliopistonkatu 5 FIN-00014 Helsinki Finland, email: hojtylli@cc.helsinki.fi
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study boundedness properties of the $q$ -mean-square operator 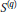{{S}^{(q)}} on 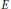$E$ -valued analytic martingales, where 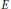$E$ is a complex quasi-Banach space and 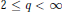$2\,\le \,q\,<\,\infty $ . We establish that a.s. finiteness of 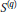${{S}^{(q)}}$ for every bounded 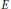$E$ -valued analytic martingale implies strong 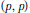$(p,\,p)$ -type estimates for 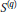${{S}^{(q)}}$ and all 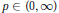$p\,\in \,(0,\,\infty )$ . Our results yield new characterizations (in terms of analytic and stochastic properties of the function 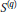${{S}^{(q)}}$ ) of the complex spaces 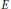$E$ that admit an equivalent $q$ -uniformly 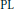$\text{PL}$ -convex quasi-norm. We also obtain a vector-valued extension (and a characterization) of part of an observation due to Bourgain and Davis concerning the 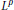${{L}^{p}}$ -boundedness of the usual square-function on scalar-valued analytic martingales.

Keywords

46B2060G46

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 2 , 01 June 1999 , pp. 221 - 230
Copyright
Copyright © Canadian Mathematical Society 1999

References

[A] Aleksandrov, A. B., Essays on non locally convex Hardy classes. Lecture Notes in Math. 864, Springer-Verlag, 1981, 1–89.Google Scholar
[BD] Bourgain, J. and Davis, W. J., Martingale transforms and complex uniform convexity. Trans. Amer.Math. Soc. 294 (1986), 501–515.Google Scholar
[B1] Burkholder, D. L., Distribution function inequalities for martingales. Ann. Probab. 1 (1973), 19–42.Google Scholar
[B2] Burkholder, D. L., A geometric characterization of Banach spaces in which martingale difference sequences are unconditional. Ann. Probab. 9 (1981), 991–1011.Google Scholar
[B3] Burkholder, D. L.,Martingale transforms and the geometry of Banach spaces. Lecture Notes in Math. 860, Springer-Verlag, 1981, 35–50.Google Scholar
[DGT] Davis, W. J., Garling, D. J. H. and Tomczak-Jaegermann, N., The complex convexity of quasi-normed linear spaces. J. Funct. Anal. 55 (1984), 110–150.Google Scholar
[DU] Diestel, J. and Uhl, J. J. Jr., Vector measures. Mathematical Surveys 15, Amer. Math. Soc., Providence, RI, 1977.Google Scholar
[D] Dilworth, S. J., Complex convexity and the geometry of Banach spaces.Math. Proc. Cambridge Philos. Soc. 99 (1986), 495–506.Google Scholar
[Ed1] Edgar, G. A., Complex martingale convergence. Lecture Notes in Math. 1166, Springer-Verlag, 1985, 38–59.Google Scholar
[Ed2] Edgar, G. A., Analytic martingale convergence. J. Funct. Anal. 69 (1986), 268–280.Google Scholar
[E] Enflo, P., Banach spaces which can be given an equivalent uniformly convex norm. Israel J. Math. 13 (1972), 281–288.Google Scholar
[G1] Garling, D. J. H., On martingales with values in a complex Banach space. Math. Proc. Cambridge Philos. Soc. 104 (1988), 399–406.Google Scholar
[G2] Garling, D. J. H., On the dual of a proper uniform algebra. Bull. LondonMath. Soc. 21 (1989), 279–284.Google Scholar
[Ge] Geiss, S., BMO -spaces and applications to extrapolation theory. Studia Math. 122 (1997), 235–274.Google Scholar
[HP] Haagerup, U. and Pisier, G., Factorization of analytic functions with values in non-commutative L1-spaces and applications. Canad. J. Math. 41 (1989), 882–906.Google Scholar
[K] König, H., Eigenvalue distributions of compact operators. Birkhäuser, 1986.Google Scholar
[L] Long, Ruilin, Martingale spaces and inequalities. Vieweg Verlag and Peking University Press, 1993.Google Scholar
[M] Mattila, K., Complex strict and uniform convexity and hyponormal operators. Math. Proc. Cambridge Philos. Soc. 96 (1984), 483–493.Google Scholar
[P] Pisier, G., Martingales with values in uniformly convex spaces. Israel J. Math. 20 (1975), 326–350.Google Scholar
[X1] Xu, Quanhua, Inégalités pour les martingales de Hardy et renormage des espaces quasinormés. C. R. Acad. Sci. Paris 306 (1988), 601–604.Google Scholar
[X2] Xu, Quanhua, Convexités uniformes et inégalités de martingales. Math. Ann. 287 (1990), 193–211.Google Scholar