Article contents
Betti Numbers and Flat Dimensions of Local Cohomology Modules
Published online by Cambridge University Press: 20 November 2018
Abstract
Assume that 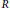 $R$ is a commutative Noetherian ring with non-zero identity,
$R$ is a commutative Noetherian ring with non-zero identity,  $\mathfrak{a}$ is an ideal of
$\mathfrak{a}$ is an ideal of 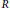 $R$ , and
$R$ , and 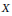 $X$ is an
$X$ is an 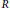 $R$ -module. In this paper, we first study the finiteness of Betti numbers of local cohomology modules
$R$ -module. In this paper, we first study the finiteness of Betti numbers of local cohomology modules 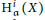 $\text{H}_{\mathfrak{a}}^{i}\left( X \right)$ . Then we give some inequalities between the Betti numbers of
$\text{H}_{\mathfrak{a}}^{i}\left( X \right)$ . Then we give some inequalities between the Betti numbers of 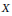 $X$ and those of its local cohomology modules. Finally, we present many upper bounds for the flat dimension of
$X$ and those of its local cohomology modules. Finally, we present many upper bounds for the flat dimension of 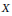 $X$ in terms of the flat dimensions of its local cohomology modules and an upper bound for the flat dimension of
$X$ in terms of the flat dimensions of its local cohomology modules and an upper bound for the flat dimension of 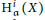 $\text{H}_{\mathfrak{a}}^{i}\left( X \right)$ in terms of the flat dimensions of the modules
$\text{H}_{\mathfrak{a}}^{i}\left( X \right)$ in terms of the flat dimensions of the modules 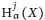 $\text{H}_{\mathfrak{a}}^{j}\left( X \right),j\ne i$ , and that of
$\text{H}_{\mathfrak{a}}^{j}\left( X \right),j\ne i$ , and that of 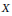 $X$ .
$X$ .
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2015
References
- 1
- Cited by

