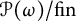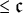Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fischer, Vera
Koelbing, Marlene
and
Wohofsky, Wolfgang
2023.
Games on Base Matrices.
Notre Dame Journal of Formal Logic,
Vol. 64,
Issue. 2,
Galgon, Geoff
2024.
Distributivity and base trees for
$P(\kappa)/ {\lt} \kappa$
.
Canadian Mathematical Bulletin,
Vol. 67,
Issue. 4,
p.
915.