Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-24T19:01:10.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Arithmetic derivatives through geometry of numbers

Part of: Diophantine approximation, transcendental number theory Geometry of numbers

Published online by Cambridge University Press:  10 December 2021

Hector Pasten
Hector Pasten*
Affiliation:
Departamento de Matemáticas, Facultad de Matemáticas, Pontificia Universidad Católica de Chile, 4860 Avenida Vicuña Mackenna, Macul, RM, Chile
*
e-mail: hpasten@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We define certain arithmetic derivatives on 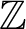$\mathbb {Z}$ that respect the Leibniz rule, are additive for a chosen equation 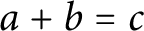$a+b=c$ , and satisfy a suitable nondegeneracy condition. Using Geometry of Numbers, we unconditionally show their existence with controlled size. We prove that any power-saving improvement on our size bounds would give a version of the 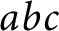$abc$ Conjecture. In fact, we show that the existence of sufficiently small arithmetic derivatives in our sense is equivalent to the 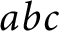$abc$ Conjecture. Our results give an explicit manifestation of an analogy suggested by Vojta in the eighties, relating Geometry of Numbers in arithmetic to derivatives in function fields and Nevanlinna theory. In addition, our construction formalizes the widespread intuition that the 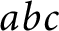$abc$ Conjecture should be related to arithmetic derivatives of some sort.

Keywords

Arithmetic derivativeabc ConjectureGeometry of Numbers

MSC classification

Primary: 11J97: Analogues of methods in Nevanlinna theory (work of Vojta et al.)
Secondary: 11H06: Lattices and convex bodies
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 4 , December 2022 , pp. 906 - 923
Check for updates
Copyright
© Canadian Mathematical Society, 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This research was supported by ANID (ex CONICYT) FONDECYT Regular grant 1190442 from Chile.

References

Barbeau, E., Remarks on an arithmetic derivative. Canad. Math. Bull. 4(1961), no. 2, 117–122.CrossRefGoogle Scholar
Bombieri, E. and Vaaler, J., On Siegel’s lemma. Invent. Math. 73(1983), no. 1, 11–32.CrossRefGoogle Scholar
Buium, A., Arithmetic differential equations. Mathematical Surveys and Monographs, 118, American Mathematical Society, Providence, RI, 2005. xxxii+310 pp.Google Scholar
de Weger, B., A + B = C and big Ш’s. Quart. J. Math. Oxford Ser. (2) 49(1998), no. 193, 105–128.CrossRefGoogle Scholar
Deitmar, A., Schemes over F1. In: van der Geer, G., Moonen, B., and Schoof, R. (eds.), Number fields and function fields—two parallel worlds, Progress in Mathematics, 239, Birkhäuser Boston, Boston, MA, 2005, pp. 87–100.Google Scholar
Faltings, G., Does there exist an arithmetic Kodaira–Spencer class? In: Pragacz, P., Szurek, M., and Wiśniewski, J. (eds.), Algebraic geometry: Hirzebruch 70 (Warsaw, 1998), Contemporary Mathematics, 241, American Mathematical Society, Providence, RI, 1999, pp. 141–146.CrossRefGoogle Scholar
Kurokawa, N., Ochiai, H., and Wakayama, M., Absolute derivations and zeta functions. Doc. Math. Extra Vol. (2003), 565–584. Kazuya Kato’s fiftieth birthday.Google Scholar
Masser, D., Abcological anecdotes. Mathematika 63(2017), no. 3, 713–714.CrossRefGoogle Scholar
Mihailescu, P., Primary cyclotomic units and a proof of Catalan’s conjecture. J. Reine Angew. Math. 572(2004), 167–195 (English summary).Google Scholar
Mingot Shelly, J., Una cuestión de la teoría de los números, Association Esp, Granada, 1911, pp. 1–12.Google Scholar
Snyder, N., An alternate proof of Mason’s theorem. Elem. Math. 55(2000), no. 3, 93–94.CrossRefGoogle Scholar
Vojta, P., Diophantine approximations and value distribution theory, Lecture Notes in Mathematics, 1239, Springer, Berlin, 1987.Google Scholar
Vojta, P., Diophantine approximation and Nevanlinna theory. In: Corvaja, P. and Gasbarri, C. (eds.) Arithmetic geometry, Lecture Notes in Mathematics, 2009, Springer, Berlin, 2011, pp. 111–224.CrossRefGoogle Scholar
Wiles, A., Modular elliptic curves and Fermat’s last theorem. Ann. of Math. (2). 141(1995), no. 3, 443–551.CrossRefGoogle Scholar