Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-11T22:14:15.115Z Has data issue: false hasContentIssue false
  • English
  • Français

An Improved Wintner Oscillation Criterion for Second Order Linear Differential Equations

Published online by Cambridge University Press:  20 November 2018

George W. Johnson  and
Jurang Yan
George W. Johnson
Affiliation:
Department of Mathematics and Statistics University of South Carolina Columbia, S.C. 29208, USA
Jurang Yan
Affiliation:
Department of Mathematics Shanxi University Taiyuan, China & Department of Mathematics And Statistics University of South Carolina Columbia, S.C. 29208USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An iterative technique is used to establish an oscillation theorem for the equation x″+ a(t)x=0 which relaxes the condition that a(t) satisfy

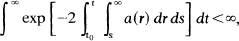
without the restriction that

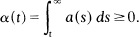
Keywords

34C10Oscillatory solutionnon-oscillatory solutionRiccati equationprincipal solutionnon-principal solution
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 27 , Issue 1 , 01 March 1984 , pp. 117 - 121
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Hartman, P., On Nonoscillatory Differential Equations of Second Order, Amer. J. Math., Vol. 74 (1952), pp. 389-400.Google Scholar
2. Hartman, P., Ordinary Differential Equations, Wiley Interscience, 1970.Google Scholar
3. Kamenev, I. V., Criteria for a Second Order Linear Equation to be Oscillatory, Related to the Existence of a Principal Solution, Differentsial'nye Uravneniya, Vol. 9, No 2 (1973), pp. 370-373.Google Scholar
4. Leighton, W. and Morse, M., Singular Quadratic Functionals, Trans. Am. Math. Soc, Vol. 40 (1936), pp. 252-286.Google Scholar
5. Wintner, A., On the Non-existence of Conjugate Points, Am. J. Math Vol. 73 (1951), pp. 368-380. Google Scholar