No CrossRef data available.
Article contents
An Elementary Probabilistic Computation of the Poisson Kernel for the n = 2 and 3 Euclidean Ball
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Direct and elementary derivation of the classical Poisson kernel for the ball in n = 2 or n = 3 dimensions starting with the usual expression 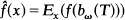 involving the brownian motion b ω, the stopping time T on the boundary, and E x the conditional expectation on paths starting at x.
involving the brownian motion b ω, the stopping time T on the boundary, and E x the conditional expectation on paths starting at x.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1984
References
1.
Gaveau, B. and Vauthier, J., Intégrales oscillantes stochastiques: L’équation de Pauli, Journal of Functional Analysis
44 (1981), pp. 388–400.Google Scholar
4.
Greiner, P., Special harmonies on the Heisenberg group, Canadian Mathematical Bulletin Vol.
23 (1980), pp. 383–393.Google Scholar

