No CrossRef data available.
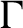 $\Gamma $ for certain
$\Gamma $ for certain 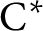 $\mathrm {C^*}$-algebras
$\mathrm {C^*}$-algebrasPublished online by Cambridge University Press: 10 January 2022
In this paper, let A be an infinite-dimensional stably finite unital simple separable
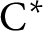 $\mathrm {C^*}$
-algebra. Let
$\mathrm {C^*}$
-algebra. Let
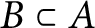 $B\subset A$
be a centrally large subalgebra in A such that B has uniform property
$B\subset A$
be a centrally large subalgebra in A such that B has uniform property
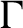 $\Gamma $
. Then we prove that A has uniform property
$\Gamma $
. Then we prove that A has uniform property
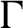 $\Gamma $
. Let
$\Gamma $
. Let
 $\Omega $
be a class of stably finite unital
$\Omega $
be a class of stably finite unital
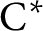 $\mathrm {C^*}$
-algebras such that for any
$\mathrm {C^*}$
-algebras such that for any
 $B\in \Omega $
, B has uniform property
$B\in \Omega $
, B has uniform property
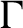 $\Gamma $
. Then we show that A has uniform property
$\Gamma $
. Then we show that A has uniform property
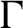 $\Gamma $
for any simple unital
$\Gamma $
for any simple unital
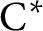 $\mathrm {C^*}$
-algebra
$\mathrm {C^*}$
-algebra
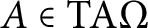 $A\in \rm {TA}\Omega $
.
$A\in \rm {TA}\Omega $
.