Let 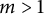$m>1$ and 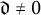$\mathfrak {d} \neq 0$ be integers such that 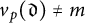$v_{p}(\mathfrak {d}) \neq m$ for any prime p. We construct a matrix 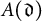$A(\mathfrak {d})$ of size 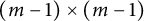$(m-1) \times (m-1)$ depending on only of 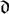$\mathfrak {d}$ with the following property: For any tame 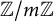$ \mathbb {Z}/m \mathbb {Z}$ -number field K of discriminant 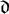$\mathfrak {d}$ , the matrix 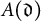$A(\mathfrak {d})$ represents the Gram matrix of the integral trace-zero form of K. In particular, we have that the integral trace-zero form of tame cyclic number fields is determined by the degree and discriminant of the field. Furthermore, if in addition to the above hypotheses, we consider real number fields, then the shape is also determined by the degree and the discriminant.