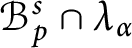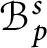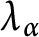Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Egueh, Yabreb
Kellay, Karim
and
Zarrabi, Mohamed
2025.
Cyclicity in Besov–Dirichlet spaces from the Corona Theorem.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 34,
Issue. 3,
p.
731.