Hostname: page-component-54dcc4c588-nx7b4 Total loading time: 0 Render date: 2025-09-11T16:28:22.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Abelian Theorems for Hardy Transformations

Published online by Cambridge University Press:  20 November 2018

R. S. Pathak  and
J. N. Pandey
R. S. Pathak
Affiliation:
Department of Math., Carleton University, Ottawa, Ontario, Canada
J. N. Pandey
Affiliation:
Department of Math., Carleton University, Ottawa, Ontario, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Initial and final value theorems for Hardy transformations 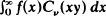and 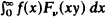of a suitably chosen function f(x) under a certain set of conditions on v and p where

1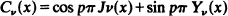

Jv (x) and Yv (x) being Bessel functions of the first and second kind, and

2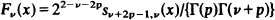

su, v (x) being Lommel's function, are proved.

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 20 , Issue 3 , 01 September 1977 , pp. 331 - 335
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Cooke, R. G., The inversion formulae of Hardy and Titchmarsh. Proc. London Math. Soc. 24 (1925), 381-420.Google Scholar
2. Erdély, A., (Editor). Tables of integral transforms, Vol. I (McGraw-Hill Book Co., Inc., New York, 1954).Google Scholar
3. Erdély, A., (Editor). Tables of integral transforms, Vol. II (McGraw-Hill Book Co., Inc., New York, 1954).Google Scholar
4. Hardy, G. H., Some formulae in the theory of Bessel functions. Proc. London Math. Soc. 23 (1925), lxi-lxiii.Google Scholar
5. Pathak, R. S., and Pandey, J. N., A distributional Hardy transformation. Proc. Camb. Phil. Soc. 76 (1974), 247-262. Google Scholar
6. Pathak, R. S., and Pandey, J. N., A distributional Hardy transformation II. Submitted for publication.Google Scholar
7. Watson, G. N., A treatise on the theory of Bessel functions (Cambridge University Press, second edn., 1962).Google Scholar
8. Widder, D. V., The Laplace Transform (Priceton University Press, 1946).Google Scholar
9. Zemanian, A. H., Some abelian theorems for the Distributional Hankel and K transformations, SIAM J. Appl. Math., Vol. 14 (1966), 1106-1111.Google Scholar