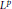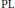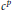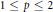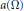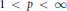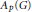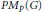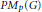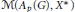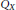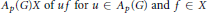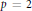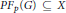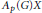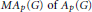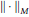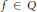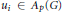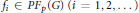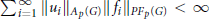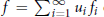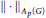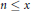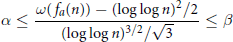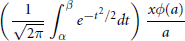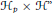Contents
Research Article
Complex Uniform Convexity and Riesz Measures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-245
-
- Article
-
- You have access
- Export citation
Éléments unipotents réguliers des sous-groupes de Levi
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 246-276
-
- Article
-
- You have access
- Export citation
Spectral Properties of the Commutator of Bergman's Projection and the Operator of Multiplication by an Analytic Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 277-292
-
- Article
-
- You have access
- Export citation
Structure of Modules Induced from Simple Modules with Minimal Annihilator
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 293-309
-
- Article
-
- You have access
- Export citation
The Geometry of Quadratic Differential Systems with a Weak Focus of Third Order
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 310-343
-
- Article
-
- You have access
- Export citation
Predual of the Multiplier Algebra of Ap (G) and Amenability
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 344-355
-
- Article
-
- You have access
- Export citation
Non-Abelian Generalizations of the Erdős-Kac Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 356-372
-
- Article
-
- You have access
- Export citation
An Elementary Proof of a Weak Exceptional Zero Conjecture
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 373-405
-
- Article
-
- You have access
- Export citation
Theta Series, Eisenstein Series and Poincaré Series over Function Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 406-430
-
- Article
-
- You have access
- Export citation
Group Actions and Singular Martingales II, The Recognition Problem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 431-448
-
- Article
-
- You have access
- Export citation