Article contents
Weakly Projective and Weakly Injective Modules
Published online by Cambridge University Press: 20 November 2018
Abstract
A module M is said to be weakly N-projective if it has a projective cover π: P(M) ↠M and for each homomorphism  : P(M) → N there exists an epimorphism σ:P(M) ↠M such that
: P(M) → N there exists an epimorphism σ:P(M) ↠M such that 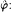 (kerσ) = 0, equivalently there exists a homomorphism
(kerσ) = 0, equivalently there exists a homomorphism 

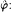 . A module M is said to be weakly projective if it is weakly N-projective for all finitely generated modules N. Weakly N-injective and weakly injective modules are defined dually. In this paper we study rings over which every weakly injective right R-module is weakly projective. We also study those rings over which every weakly projective right module is weakly injective. Among other results, we show that for a ring R the following conditions are equivalent:
. A module M is said to be weakly projective if it is weakly N-projective for all finitely generated modules N. Weakly N-injective and weakly injective modules are defined dually. In this paper we study rings over which every weakly injective right R-module is weakly projective. We also study those rings over which every weakly projective right module is weakly injective. Among other results, we show that for a ring R the following conditions are equivalent:
(1) R is a left perfect and every weakly projective right R-module is weakly injective.
(2) R is a direct sum of matrix rings over local QF-rings.
(3) R is a QF-ring such that for any indecomposable projective right module eR and for any right ideal I, soc(eR/eI) = (eR/eJ)n for some positive integer n.
(4) R is right artinian ring and every weakly injective right R-module is weaklyprojective.
(5) Every weakly projective right R-module is weakly injective and every weakly injective right R-module is weakly projective.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1994
References
- 3
- Cited by

