No CrossRef data available.
Article contents
Values of the Dedekind Eta Function at Quadratic Irrationalities: Corrigendum
Published online by Cambridge University Press: 20 November 2018
Abstract
Habib Muzaffar of Carleton University has pointed out to the authors that in their paper  $\left[ \text{A} \right]$ only the result
$\left[ \text{A} \right]$ only the result
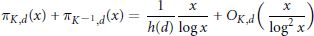 $${{\pi }_{K,d}}\left( x \right)\,+\,{{\pi }_{{{K}^{-1}},d}}\left( x \right)\,=\,\frac{1}{h\left( d \right)}\,\frac{x}{\log x}\,+\,{{O}_{K,d}}\left( \frac{x}{{{\log }^{2}}x} \right)$$
$${{\pi }_{K,d}}\left( x \right)\,+\,{{\pi }_{{{K}^{-1}},d}}\left( x \right)\,=\,\frac{1}{h\left( d \right)}\,\frac{x}{\log x}\,+\,{{O}_{K,d}}\left( \frac{x}{{{\log }^{2}}x} \right)$$
follows from the prime ideal theorem with remainder for ideal classes, and not the stronger result
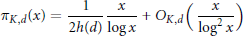 $${{\pi }_{K,d}}\left( x \right)\,=\,\frac{1}{2h\left( d \right)}\,\frac{x}{\log \,x}\,+\,{{O}_{K,d}}\left( \frac{x}{{{\log }^{2}}\,x} \right)$$
$${{\pi }_{K,d}}\left( x \right)\,=\,\frac{1}{2h\left( d \right)}\,\frac{x}{\log \,x}\,+\,{{O}_{K,d}}\left( \frac{x}{{{\log }^{2}}\,x} \right)$$
stated in Lemma 5.2. This necessitates changes in Sections 5 and 6 of  $\left[ \text{A} \right]$ . The main results of the paper are not affected by these changes. It should also be noted that, starting on page 177 of
$\left[ \text{A} \right]$ . The main results of the paper are not affected by these changes. It should also be noted that, starting on page 177 of 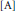 $\left[ \text{A} \right]$ , each and every occurrence of
$\left[ \text{A} \right]$ , each and every occurrence of 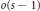 $o\left( s-1 \right)$ should be replaced by
$o\left( s-1 \right)$ should be replaced by 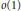 $o\left( 1 \right)$ .
$o\left( 1 \right)$ .
Sections 5 and 6 of 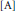 $\left[ \text{A} \right]$ have been rewritten to incorporate the abovementioned correction and are given below. They should replace the original Sections 5 and 6 of
$\left[ \text{A} \right]$ have been rewritten to incorporate the abovementioned correction and are given below. They should replace the original Sections 5 and 6 of 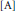 $\left[ \text{A} \right]$ .
$\left[ \text{A} \right]$ .
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2001

