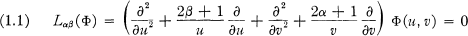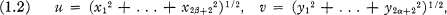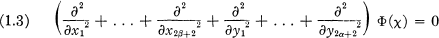Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
McCoy, Peter A
1979.
Polynomial approximation of generalized biaxisymmetric potentials.
Journal of Approximation Theory,
Vol. 25,
Issue. 2,
p.
153.