Article contents
Topological Extension Properties and Projective Covers
Published online by Cambridge University Press: 20 November 2018
Extract
Introduction. All spaces considered in this paper are assumed to be (Hausdorff) completely regular, and all maps are continuous. Let 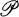 be a topological property of spaces. We shall identify
be a topological property of spaces. We shall identify 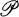 with the class of spaces having
with the class of spaces having 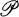 . A space having
. A space having 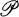 is called a
is called a 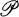 -space, and a subspace of a
-space, and a subspace of a 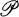 -space is called a
-space is called a 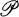 -regular space. The class of
-regular space. The class of 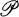 -regular spaces is denoted by R(
-regular spaces is denoted by R(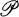 ). Following [37], we call a closed hereditary, productive, topological property
). Following [37], we call a closed hereditary, productive, topological property 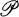 such that each
such that each 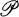 -regular space has a
-regular space has a 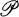 -regular compactification a topological extension property, or simply, an extension property. In this paper, we restrict our attention to extension properties
-regular compactification a topological extension property, or simply, an extension property. In this paper, we restrict our attention to extension properties 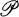 satisfying the following axioms:
satisfying the following axioms:
(A1) The two-point discrete space has 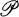 .
.
(A2) If each 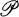 -regular space of nonmeasurable cardinal has
-regular space of nonmeasurable cardinal has 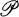 , then
, then 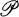 = R(
= R(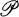 ).
).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1982
References
- 4
- Cited by

