No CrossRef data available.
Article contents
Tilings of Normed Spaces
Published online by Cambridge University Press: 20 November 2018
Abstract
By a tiling of a topological linear space  $X$ , we mean a covering of
$X$ , we mean a covering of  $X$ by at least two closed convex sets, called tiles, whose nonempty interiors are pairwise disjoint. Study of tilings of infinite dimensional spaces was initiated in the 1980's with pioneer papers by V. Klee. We prove some general properties of tilings of locally convex spaces, and then apply these results to study the existence of tilings of normed and Banach spaces by tiles possessing certain smoothness or rotundity properties. For a Banach space
$X$ by at least two closed convex sets, called tiles, whose nonempty interiors are pairwise disjoint. Study of tilings of infinite dimensional spaces was initiated in the 1980's with pioneer papers by V. Klee. We prove some general properties of tilings of locally convex spaces, and then apply these results to study the existence of tilings of normed and Banach spaces by tiles possessing certain smoothness or rotundity properties. For a Banach space  $X$ , our main results are the following.
$X$ , our main results are the following.
-
(i)
 $X$ admits no tiling by Fréchet smooth bounded tiles.
$X$ admits no tiling by Fréchet smooth bounded tiles. -
(ii) If
 $X$ is locally uniformly rotund
$X$ is locally uniformly rotund 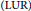 $\left( \text{LUR} \right)$ , it does not admit any tiling by balls.
$\left( \text{LUR} \right)$ , it does not admit any tiling by balls. -
(iii) On the other hand, some
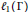 ${{\ell }_{1}}\left( \Gamma\right)$ spaces,
${{\ell }_{1}}\left( \Gamma\right)$ spaces,  $\Gamma $ uncountable, do admit a tiling by pairwise disjoint
$\Gamma $ uncountable, do admit a tiling by pairwise disjoint 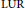 $\text{LUR}$ bounded tiles.
$\text{LUR}$ bounded tiles.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2017
References
- 1
- Cited by

