Article contents
Symplectic Geometry of the Moduli Space of Flat Connections on a Riemann Surface: Inductive Decompositions and Vanishing Theorems
Published online by Cambridge University Press: 20 November 2018
Abstract
This paper treats the moduli space 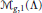 ${{\mathcal{M}}_{g,1}}(\Lambda)$ of representations of the fundamental group of a Riemann surface of genus
${{\mathcal{M}}_{g,1}}(\Lambda)$ of representations of the fundamental group of a Riemann surface of genus  $g$ with one boundary component which send the loop around the boundary to an element conjugate to exp
$g$ with one boundary component which send the loop around the boundary to an element conjugate to exp 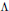 $\Lambda$ , where
$\Lambda$ , where 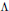 $\Lambda$ is in the fundamental alcove of a Lie algebra. We construct natural line bundles over
$\Lambda$ is in the fundamental alcove of a Lie algebra. We construct natural line bundles over 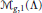 ${{\mathcal{M}}_{g,1}}(\Lambda)$ and exhibit natural homology cycles representing the Poincaré dual of the first Chern class. We use these cycles to prove differential equations satisfied by the symplectic volumes of these spaces. Finally we give a bound on the degree of a nonvanishing element of a particular subring of the cohomology of the moduli space of stable bundles of coprime rank
${{\mathcal{M}}_{g,1}}(\Lambda)$ and exhibit natural homology cycles representing the Poincaré dual of the first Chern class. We use these cycles to prove differential equations satisfied by the symplectic volumes of these spaces. Finally we give a bound on the degree of a nonvanishing element of a particular subring of the cohomology of the moduli space of stable bundles of coprime rank  $k$ and degree
$k$ and degree 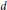 $d$ .
$d$ .
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2000
References
- 2
- Cited by

