Article contents
Sur les Ensembles de Sommets Indépendants Dans les Graphes Chromatiques Minimaux
Published online by Cambridge University Press: 20 November 2018
Extract
f(n, k) sera l'entier maximum t tel qu'il existe un graphe G ayant les propriétés suivantes:
-
(a) G possède n sommets;
-
(b) le nombre chromatique de G est égal à k;
-
(c) Gest minimal par rapport à la propriété (b); c'est-à-dire, la suppression ede n'importe quelle arête rend G(k – 1)-colorable;
-
(d) il existe t sommets indépendants de G, c'est-à-dire dont nulle paire ne se joigne par une arête.
Un graphe sera k-minimal s'il possède les propriétés (b) et (c). Puisque les graphes 3-minimaux sont tous des polygones impairs, il s'ensuit que f(n, 3) = [n/2] (n = 3, 5, 7, …), Il y a quelque temps T. Gallai a posé la conjecture:
1.1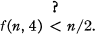
M. Simonovits a réfuté l'inégalité stricte dans (1.1) en prouvant que
1.2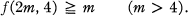
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1969
- 8
- Cited by

