No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Averages in weighted spaces
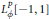 $L_{\phi }^{p}[-1,1]$
defined by additions on
$L_{\phi }^{p}[-1,1]$
defined by additions on 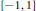 $[-1,\,1]$ will be shown to satisfy strong converse inequalities of type
$[-1,\,1]$ will be shown to satisfy strong converse inequalities of type  $\text{A}$ and
$\text{A}$ and  $\text{B}$ with appropriate
$\text{B}$ with appropriate 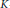 $K$-functionals. Results for higher levels of smoothness are achieved by combinations of averages. This yields, in particular, strong converse inequalities of type
$K$-functionals. Results for higher levels of smoothness are achieved by combinations of averages. This yields, in particular, strong converse inequalities of type 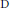 $\text{D}$ between
$\text{D}$ between 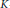 $K$-functionals and suitable difference operators.
$K$-functionals and suitable difference operators.