Published online by Cambridge University Press: 20 November 2018
We consider the stochastic difference equation 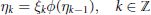 ${{\eta }_{k}}\,=\,{{\xi }_{k}}\phi \left( {{\eta }_{k-1}} \right),\,\,k\,\in \,\mathbb{Z}$ on a locally compact group
${{\eta }_{k}}\,=\,{{\xi }_{k}}\phi \left( {{\eta }_{k-1}} \right),\,\,k\,\in \,\mathbb{Z}$ on a locally compact group 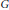 $G$, where
$G$, where 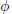 $\phi $ is an automorphism of
$\phi $ is an automorphism of 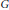 $G$,
$G$, 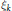 ${{\xi }_{K}}$ are given
${{\xi }_{K}}$ are given 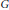 $G$-valued random variables, and
$G$-valued random variables, and 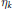 ${{\eta }_{k}}$ are unknown
${{\eta }_{k}}$ are unknown 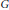 $G$-valued random variables. This equation was considered by Tsirelson and Yor on a one-dimensional torus. We consider the case when
$G$-valued random variables. This equation was considered by Tsirelson and Yor on a one-dimensional torus. We consider the case when 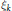 ${{\xi }_{K}}$ have a common law
${{\xi }_{K}}$ have a common law  $\mu $ and prove that if
$\mu $ and prove that if 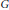 $G$ is a distal group and
$G$ is a distal group and 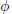 $\phi $ is a distal automorphism of
$\phi $ is a distal automorphism of 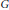 $G$ and if the equation has a solution, then extremal solutions of the equation are in one-to-one correspondence with points on the coset space
$G$ and if the equation has a solution, then extremal solutions of the equation are in one-to-one correspondence with points on the coset space 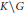 $K\backslash G$ for some compact subgroup
$K\backslash G$ for some compact subgroup 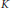 $K$ of
$K$ of 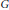 $G$ such that
$G$ such that  $\mu $ is supported on
$\mu $ is supported on 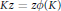 $Kz\,=\,z\phi \left( K \right)$ for any
$Kz\,=\,z\phi \left( K \right)$ for any  $z$ in the support of
$z$ in the support of  $\mu $. We also provide a necessary and sufficient condition for the existence of solutions to the equation.
$\mu $. We also provide a necessary and sufficient condition for the existence of solutions to the equation.