Published online by Cambridge University Press: 07 January 2019
In this paper we study spectral properties of the Dirichlet-to-Neumann map on differential forms obtained by a slight modification of the definition due to Belishev and Sharafutdinov. The resulting operator 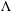 $\unicode[STIX]{x039B}$ is shown to be self-adjoint on the subspace of coclosed forms and to have purely discrete spectrum there. We investigate properties of eigenvalues of
$\unicode[STIX]{x039B}$ is shown to be self-adjoint on the subspace of coclosed forms and to have purely discrete spectrum there. We investigate properties of eigenvalues of 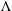 $\unicode[STIX]{x039B}$ and prove a Hersch–Payne–Schiffer type inequality relating products of those eigenvalues to eigenvalues of the Hodge Laplacian on the boundary. Moreover, non-trivial eigenvalues of
$\unicode[STIX]{x039B}$ and prove a Hersch–Payne–Schiffer type inequality relating products of those eigenvalues to eigenvalues of the Hodge Laplacian on the boundary. Moreover, non-trivial eigenvalues of 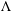 $\unicode[STIX]{x039B}$ are always at least as large as eigenvalues of the Dirichlet-to-Neumann map defined by Raulot and Savo. Finally, we remark that a particular case of
$\unicode[STIX]{x039B}$ are always at least as large as eigenvalues of the Dirichlet-to-Neumann map defined by Raulot and Savo. Finally, we remark that a particular case of 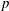 $p$-forms on the boundary of a
$p$-forms on the boundary of a 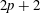 $2p+2$-dimensional manifold shares many important properties with the classical Steklov eigenvalue problem on surfaces.
$2p+2$-dimensional manifold shares many important properties with the classical Steklov eigenvalue problem on surfaces.