Hostname: page-component-54dcc4c588-ff9ft Total loading time: 0 Render date: 2025-10-08T06:27:12.193Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral Inclusion and C.N.E.

Published online by Cambridge University Press:  20 November 2018

A. R. Lubin
A. R. Lubin*
Affiliation:
Illinois Institute of Technology, Chicago, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. An n-tuple S = (S 1, …, Sn ) of commuting bounded linear operators on a Hilbert space H is said to have commuting normal extension if and only if there exists an n-tuple N = (N 1, …, Nn ) of commuting normal operators on some larger Hilbert space K ⊃ H with the restrictions Ni|H = Si, i = 1, …, n. If we take

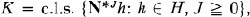
the minimal reducing subspace of N containing H, then N is unique up to unitary equivalence and is called the c.n.e. of S. (Here J denotes the multi-index (j 1, …, jn ) of nonnegative integers and N *J = N 1 *jl … Nn *jn and we emphasize that c.n.e. denotes minimal commuting normal extension.) If n = 1, then S 1 = S is called subnormal and N 1 = N its minimal normal extension (m.n.e.).

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 4 , 01 August 1982 , pp. 883 - 887
Copyright
Copyright © Canadian Mathematical Society 1982

References

References>

1. Abrahamse, M. B., Commuting subnormal operators, Ill. J. Math. 22 (1978), 171–176.Google Scholar
2. Arveson, W., Subalgebras of C*-algebras II, Acta Math. 128 (1972), 271–308.Google Scholar
3. Bastian, J. J., A decomposition of weighted translation operators, Trans. Math. Soc. 224 (1976).Google Scholar
4. Bram, J., Subnormal operators, Duke Math. J. 22 (1955), 75–94.Google Scholar
5. Bunce, J., and Deddens, J., On the normal spectrum of a subnormal operator, Proc. Amer. Math. Soc. 63 (1977), 107–110.Google Scholar
6. Curto, R. E., Spectral inclusion for doubly commuting subnormal n-tuples, (preprint).Google Scholar
7. Dixmier, J., Les algebres d'operateurs dans l'espace Hilbertien (Gauthier-Villars, Paris, 1969).Google Scholar
8. Halmos, P. R., Normal dilations and extensions of operators, Summa. Brasil. Math. 2 (1950), 125–134.Google Scholar
9. Halmos, P. R., A Hilbert space problem book (Van Nostrand, Princeton, 1967).Google Scholar
10. Hastings, W., Commuting subnormal operators simultaneously quasisimilar to unilateral shifts, Ill. J. Math. 22 (1978), 506–519.Google Scholar
11. Janas, J., Lifting commutants of subnormal operators and spectral inclusion, Bull. Acad. Polon. 26 (1978).Google Scholar
12. Ito, T., On the commutative family of subnormal operators, J. Fac. Sci. Hokkaido, Sec. I 14 (1958), 1–15.Google Scholar
13. Lubin, A. R., Weighted shifts and products of subnormal operators, Ind. U. Math. J. 26 (1977), 839–845.Google Scholar
14. Lubin, A. R., A subnormal semigroup without normal extension, Proc. Amer. Math. Soc. 68 (1978), 133–135.Google Scholar
15. Lubin, A. R., Extensions of commuting subnormals, Lecture Notes in Math. 693 (Springer- Verlag), 115–128.Google Scholar
16. Waelbroeck, L., Le calcule symbolique dans les algebras commutatives, J. Math. Pures Appl. 33 (1954), 147–186.Google Scholar