Article contents
Some Convexity Results for the Cartan Decomposition
Published online by Cambridge University Press: 20 November 2018
Abstract
In this paper, we consider the set 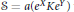 $\text{S}=a\left( {{e}^{X}}K{{e}^{Y}} \right)$ where
$\text{S}=a\left( {{e}^{X}}K{{e}^{Y}} \right)$ where 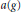 $a\left( g \right)$ is the abelian part in the Cartan decomposition of
$a\left( g \right)$ is the abelian part in the Cartan decomposition of  $g$ . This is exactly the support of the measure intervening in the product formula for the spherical functions on symmetric spaces of noncompact type. We give a simple description of that support in the case of
$g$ . This is exactly the support of the measure intervening in the product formula for the spherical functions on symmetric spaces of noncompact type. We give a simple description of that support in the case of 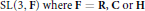 $\text{SL}\left( 3,\,\mathbf{F} \right)\,\text{where}\,\mathbf{F}\,=\,\mathbf{R},\,\mathbf{C}\,\text{or}\,\mathbf{H}$ . In particular, we show that
$\text{SL}\left( 3,\,\mathbf{F} \right)\,\text{where}\,\mathbf{F}\,=\,\mathbf{R},\,\mathbf{C}\,\text{or}\,\mathbf{H}$ . In particular, we show that  $\text{S}$ is convex.
$\text{S}$ is convex.
We also give an application of our result to the description of singular values of a product of two arbitrary matrices with prescribed singular values.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2003
References
- 1
- Cited by

