Article contents
Smoothness of Quotients Associated With a Pair of Commuting Involutions
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $\sigma $ ,
$\sigma $ , 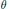 $\theta $ be commuting involutions of the connected semisimple algebraic group
$\theta $ be commuting involutions of the connected semisimple algebraic group 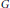 $G$ where
$G$ where 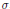 $\sigma$ ,
$\sigma$ , 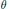 $\theta $ and
$\theta $ and 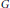 $G$ are defined over an algebraically closed field
$G$ are defined over an algebraically closed field 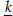 $\underset{\scriptscriptstyle-}{k},$ char
$\underset{\scriptscriptstyle-}{k},$ char 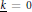 $\underline{k}$ =0. Let
$\underline{k}$ =0. Let 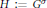 $H:={{G}^{\sigma }}$ and
$H:={{G}^{\sigma }}$ and 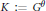 $K:={{G}^{\theta }}$ be the fixed point groups. We have an action
$K:={{G}^{\theta }}$ be the fixed point groups. We have an action 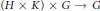 $\left( H\,\times \,K \right)\,\times \,G\,\to \,G$ , where
$\left( H\,\times \,K \right)\,\times \,G\,\to \,G$ , where 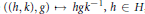 $\left( \left( h,\,k \right),\,g \right)\,\mapsto \,hg{{k}^{-1}},\,h\,\in \,H$ ,
$\left( \left( h,\,k \right),\,g \right)\,\mapsto \,hg{{k}^{-1}},\,h\,\in \,H$ , 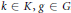 $k\,\in \,K,g\,\in \,G$ . Let
$k\,\in \,K,g\,\in \,G$ . Let 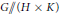 $G\,//\,\left( H\,\times \,K \right)$ denote the categorical quotient Spec
$G\,//\,\left( H\,\times \,K \right)$ denote the categorical quotient Spec 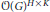 $\mathcal{O}{{(G)}^{H\times K}}$ . We determine when this quotient is smooth. Our results are a generalization of those of Steinberg [Ste75], Pittie [Pit72] and Richardson [Ric82] in the symmetric case where
$\mathcal{O}{{(G)}^{H\times K}}$ . We determine when this quotient is smooth. Our results are a generalization of those of Steinberg [Ste75], Pittie [Pit72] and Richardson [Ric82] in the symmetric case where 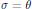 $\sigma \,=\,\theta $ and
$\sigma \,=\,\theta $ and 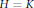 $H\,=K$ .
$H\,=K$ .
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2004
References
- 4
- Cited by

