Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kuo, Tzee-Char
1999.
Inspiring exercises for undergraduates.
International Journal of Mathematical Education in Science and Technology,
Vol. 30,
Issue. 6,
p.
811.
Fukui, Toshizumi
Kuo, Tzee-Char
and
Paunescu, Laurentiu
2001.
Constructing blow-analytic isomorphisms.
Annales de l'Institut Fourier,
Vol. 51,
Issue. 4,
p.
1071.
Herrera Govantes, F.J.
Olalla Acosta, M.A.
and
Spivakovsky, M.
2007.
Valuations in algebraic field extensions.
Journal of Algebra,
Vol. 312,
Issue. 2,
p.
1033.
Lucas, F.
Madden, J.
Schaub, D.
and
Spivakovsky, M.
2014.
Approximate roots of a valuation and the Pierce-Birkhoff conjecture.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 21,
Issue. 2,
p.
259.
Poteaux, Adrien
and
Rybowicz, Marc
2015.
Improving Complexity Bounds for the Computation of Puiseux Series over Finite Fields.
p.
299.

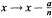 , eliminates the second term of the polynomial x
, eliminates the second term of the polynomial x