Hostname: page-component-54dcc4c588-mz6gc Total loading time: 0 Render date: 2025-09-17T07:06:47.474Z Has data issue: false hasContentIssue false
  • English
  • Français

Sieve-Generated Sequences

Published online by Cambridge University Press:  20 November 2018

M. C. Wunderlich
M. C. Wunderlich*
Affiliation:
State University of New York, Buffalo
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We shall consider a generalization of the sieve process introduced by W. E. Briggs (1) in 1963. Let A (1) be the sequence {ak (1)}, where ak (1) = k + 1, so that A (1) = {2, 3, 4, … }. Suppose inductively that A (1), A (2), … , A (n) has been defined. 4(n+1) will be defined from A(n) = {a1(n) , a2 (n), a3 (n), …} in the following manner: For each integer t ⩾ 0, choose an arbitrary element αt(n) from the set 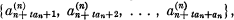where an = an(n) , and delete the elements αt(n) from A(n) to form A(n+1). The sequence A is defined to be the sequence {an}. It is also the set-theoretic intersection of all the sequences A(n), n — 1, 2, … . Let 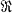be the class of all sequences that can be generated by this sieve process.

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 18 , 1966 , pp. 291 - 299
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Briggs, W. E., Prime-like sequences generated by a sieve process, Duke Math. J., 30 (1963), 297–312.Google Scholar
2. Erdös, P. and Jabotinsky, E., On sequences generated by a sieving process, Proc. Konink. Nederl. Akad. von Wetensch., 61 (1958), 297–312.Google Scholar
3. Gardiner, V., Lazarus, R., Metropolis, M., and Ulam, S., On certain sequences of integers defined by sieves, Math. Magazine, 81 (1957/58), 1-3.Google Scholar
4. Hawkins, D., The random sieve, Math. Magazine, 81 (1957/58), 1–3.Google Scholar
5. Hawkins, D. and Briggs, W. E., The lucky number theorem, Math. Magazine, 81 (1957/58), 277–280.Google Scholar
6. Lachapelle, B., L'espérance mathématique du nombre de nombres premiers aléatoires inférieurs ou égaux à x, Can. Math. Bull., 4 (1961), 139–142.Google Scholar