Article contents
Short Time Behavior of Solutions to Linear and Nonlinear Schrödinger Equations
Published online by Cambridge University Press: 20 November 2018
Abstract
We examine the fine structure of the short time behavior of solutions to various linear and nonlinear Schrödinger equations 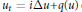 ${{u}_{t}}=i\Delta u+q(u)$ on
${{u}_{t}}=i\Delta u+q(u)$ on 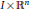 $I\times {{\mathbb{R}}^{n}}$ , with initial data
$I\times {{\mathbb{R}}^{n}}$ , with initial data  $u(0,x)=f(x)$ . Particular attention is paid to cases where
$u(0,x)=f(x)$ . Particular attention is paid to cases where 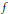 $f$ is piecewise smooth, with jump across an
$f$ is piecewise smooth, with jump across an 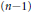 $(n-1)$ -dimensional surface. We give detailed analyses of Gibbs-like phenomena and also focusing effects, including analogues of the Pinsky phenomenon. We give results for general
$(n-1)$ -dimensional surface. We give detailed analyses of Gibbs-like phenomena and also focusing effects, including analogues of the Pinsky phenomenon. We give results for general  $n$ in the linear case. We also have detailed analyses for a broad class of nonlinear equations when
$n$ in the linear case. We also have detailed analyses for a broad class of nonlinear equations when 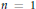 $n=1$ and 2, with emphasis on the analysis of the first order correction to the solution of the corresponding linear equation. This work complements estimates on the error in this approximation.
$n=1$ and 2, with emphasis on the analysis of the first order correction to the solution of the corresponding linear equation. This work complements estimates on the error in this approximation.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2008
References
- 1
- Cited by

