Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1998.
Algebra in the Stone-Čech Compactification.
p.
455.
Hindman, Neil
and
Strauss, Dona
2002.
Recent Progress in General Topology II.
p.
227.

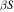 of a topological semigroup
of a topological semigroup  , and the compactification is
, and the compactification is 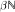 . Included is the statement that some set
. Included is the statement that some set 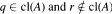 .
.
