Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Schep, Anton R.
2010.
Products and factors of Banach function spaces.
Positivity,
Vol. 14,
Issue. 2,
p.
301.
Sánchez Pérez, E. A.
2014.
Factorization Theorems for Multiplication Operators on Banach Function Spaces.
Integral Equations and Operator Theory,
Vol. 80,
Issue. 1,
p.
117.
Kolwicz, Paweł
Leśnik, Karol
and
Maligranda, Lech
2014.
Pointwise products of some Banach function spaces and factorization.
Journal of Functional Analysis,
Vol. 266,
Issue. 2,
p.
616.
Leśnik, Karol
and
Maligranda, Lech
2016.
Interpolation of abstract Cesàro, Copson and Tandori spaces.
Indagationes Mathematicae,
Vol. 27,
Issue. 3,
p.
764.
Kolwicz, Paweł
Leśnik, Karol
and
Maligranda, Lech
2019.
Symmetrization, factorization and arithmetic of quasi-Banach function spaces.
Journal of Mathematical Analysis and Applications,
Vol. 470,
Issue. 2,
p.
1136.
Agud, Lucia
Calabuig, Jose Manuel
Juan, Maria Aranzazu
and
Sánchez Pérez, Enrique A.
2020.
Banach Lattice Structures and Concavifications in Banach Spaces.
Mathematics,
Vol. 8,
Issue. 1,
p.
127.
Berezhnoi, E. I.
2021.
The Calderón construction for a couple of global Morrey spaces.
Izvestiya: Mathematics,
Vol. 85,
Issue. 5,
p.
833.
Berezhnoi, Evgenii Ivanovich
2021.
Конструкция Кальдерона для пары глобальных пространств Морри.
Известия Российской академии наук. Серия математическая,
Vol. 85,
Issue. 5,
p.
5.
Berezhnoi, Evgenii I.
2022.
TWO EMBEDDING THEOREMS FOR INTERPOLATION FUNCTORS ON COUPLES OF GLOBAL MORREY SPACES.
Journal of Mathematical Sciences,
Vol. 266,
Issue. 2,
p.
258.
Berezhnoi, Evgenii I.
2022.
Multipliers for local Morrey spaces.
Positivity,
Vol. 26,
Issue. 5,
Berezhnoi, E. I.
2023.
Multipliers for the Calderón Construction.
Functional Analysis and Its Applications,
Vol. 57,
Issue. 2,
p.
87.
Berezhnoi, Evgenii Ivanovich
2023.
Мультипликаторы для конструкции Кальдерона.
Функциональный анализ и его приложения,
Vol. 57,
Issue. 2,
p.
3.
Berezhnoi, Evgenii I.
2023.
Multipliers for global Morrey spaces.
Positivity,
Vol. 27,
Issue. 3,
Berezhnoi, E. I.
2025.
Multipliers for the Calderón–Lozanovskii Construction.
Mathematical Notes,
Vol. 117,
Issue. 1-2,
p.
195.
Kiwerski, Tomasz
and
Tomaszewski, Jakub
2025.
A few last words on pointwise multipliers of Calderón–Lozanovskiĭ spaces.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 204,
Issue. 5,
p.
2147.
Berezhnoi, Evgenii I.
2025.
Multipliers for Pairs of Grand and Small Lebesgue Space for $$p \in (1, \infty )$$.
Potential Analysis,
Vol. 63,
Issue. 3,
p.
1235.
Berezhnoi, Evgenii Ivanovich
2025.
Мультипликаторы для конструкции Кальдерона-Лозановского.
Математические заметки,
Vol. 117,
Issue. 2,
p.
181.
Berezhnoi, Evgenii I.
2025.
Grand and small spaces based on the Calderón’s construction.
Analysis and Mathematical Physics,
Vol. 15,
Issue. 4,
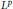 ${{L}^{p}}$ spaces are investigated. It is natural to extend the Gagliardo theorem on the Schur test and the Rubio de Francia theorem on factorization of the Muckenhoupt
${{L}^{p}}$ spaces are investigated. It is natural to extend the Gagliardo theorem on the Schur test and the Rubio de Francia theorem on factorization of the Muckenhoupt 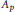 ${{A}_{p}}$ weights to reflexive Orlicz spaces. However, it turns out that for the scales far from
${{A}_{p}}$ weights to reflexive Orlicz spaces. However, it turns out that for the scales far from 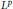 ${{L}^{p}}$ -spaces this is impossible. For the concrete integral operators it is shown that factorization theorems and the Schur test in some reflexive Orlicz spaces are not valid. Representation theorems for the Calderón–Lozanovskiĭ construction are involved in the proofs.
${{L}^{p}}$ -spaces this is impossible. For the concrete integral operators it is shown that factorization theorems and the Schur test in some reflexive Orlicz spaces are not valid. Representation theorems for the Calderón–Lozanovskiĭ construction are involved in the proofs.
