Hostname: page-component-857557d7f7-ktsnh Total loading time: 0 Render date: 2025-11-22T11:56:14.100Z Has data issue: false hasContentIssue false
  • English
  • Français

Relatively Finitely Determined Implies Relatively Very Weak Bernoulli

Published online by Cambridge University Press:  20 November 2018

M. Rahe
M. Rahe*
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

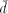In the isomorphism theory of Bernoulli shifts, the or Hamming distance plays an important role. Two finite state stationary processes are close in the 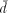metric if, on the average, strings from one process can be matched with strings from the other process so that their outputs agree with high frequency. Since such agreement must hold in the arbitrarily distant future, it might at first seem difficult to control the pairing.

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 30 , Issue 3 , 01 June 1978 , pp. 531 - 548
Copyright
Copyright © Canadian Mathematical Society 1978

References

1. Thouvenot, Jean-Paul, Quelques propriétés des systèmes dynamiques qui se décomposent en un produit de deux systèmes dont Vun est un schéma de Bernoulli, Israel J. Math. 21 (1975), 177–207.Google Scholar
2. Ornstein, D. S. and Weiss, B., Finitely determined implies very weak Bernoulli, Israel J. Math. 17 (1974), 94–104.Google Scholar
3. Ornstein, D. S., Ergodic theory, randomness, and dynamical systems (Yale Mathematical Monographs 5, New Haven, 1974).Google Scholar
4. Smorodinsky, M., Ergodic theory, entropy, Lecture Notes in Mathematics 214+ (Springer- Verlag, New York, 1971).Google Scholar