Article contents
Relative Kloosterman Integrals for GL(3): II
Published online by Cambridge University Press: 20 November 2018
Abstract
Let G′ be a quasi–split reductive group over a local field F, ƒ′ the characteristic function of a maximal compact subgroup K′ of G′, N′ a maximal unipotent subgroup of G′. We consider the orbits of maximal dimension for the action of N′ × N′ on G′ and the weighted orbital integral of f′ on such an orbit, the weight being a generic character. The resulting integral, we call a Kloosterman integral. A relative version of this construction is to consider a symmetric space S associated to a quasi-split group G, a maximal unipotent subgroup N of G, a maximal compact K of G and the orbits of maximal dimension for the action of N on S. The weighted orbital integral of the characteristic function f of K ∩ S on such an orbit is what we call a relative Kloosterman integral; the weight is an appropriate character of N. We conjecture that a relative Kloosterman integral is actually a Kloosterman integral for an appropriate group G′. We prove the conjecture in a simple case: E is an unramified quadratic extension of F,G is GL(3, E), S is the set of 3 × 3 matrices s such that 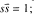 the group G′ is then the quasi-split unitary group in three variables.
the group G′ is then the quasi-split unitary group in three variables.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1992
References
- 6
- Cited by

