Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1998.
Handbook of Recursive Mathematics - Volume 1: Recursive Model Theory.
Vol. 138,
Issue. ,
p.
515.

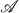 be a countable atomless Boolean algebra and let
be a countable atomless Boolean algebra and let 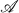 which is recursive in
which is recursive in 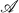 and which destroys all suprema and infima of
and which destroys all suprema and infima of 