Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ANNABY, M. H.
BUTERIN, S. A.
and
FREILING, G.
2009.
SAMPLING AND BIRKHOFF REGULAR PROBLEMS.
Journal of the Australian Mathematical Society,
Vol. 87,
Issue. 3,
p.
289.
Annaby, Mahmoud H.
and
Asharabi, Rashad M.
2012.
Computing eigenvalues of Sturm–Liouville problems by Hermite interpolations.
Numerical Algorithms,
Vol. 60,
Issue. 3,
p.
355.
Tharwat, Mohammed M
and
Bhrawy, Ali H
2012.
Computation of eigenvalues of discontinuous dirac system using Hermite interpolation technique.
Advances in Difference Equations,
Vol. 2012,
Issue. 1,
Tharwat, M. M.
and
Al-Harbi, S. M.
2013.
Approximation of Eigenvalues of Sturm-Liouville Problems by Using Hermite Interpolation.
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Annaby, M.H.
and
Tharwat, M.M.
2013.
The Hermite interpolation approach for computing eigenvalues of Dirac systems.
Mathematical and Computer Modelling,
Vol. 57,
Issue. 9-10,
p.
2459.
Tharwat, Mohammed M
2013.
Computing eigenvalues and Hermite interpolation for Dirac systems with eigenparameter in boundary conditions.
Boundary Value Problems,
Vol. 2013,
Issue. 1,
Tharwat, M. M.
Bhrawy, A. H.
and
Alofi, A. S.
2013.
Computing Eigenvalues of Discontinuous Sturm-Liouville Problems with Eigenparameter in All Boundary Conditions Using Hermite Approximation.
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Asharabi, R. M.
and
Prestin, J.
2015.
A Modification of Hermite Sampling with a Gaussian Multiplier.
Numerical Functional Analysis and Optimization,
Vol. 36,
Issue. 4,
p.
419.
Asharabi, R. M.
2016.
Generalized sinc-Gaussian sampling involving derivatives.
Numerical Algorithms,
Vol. 73,
Issue. 4,
p.
1055.
Asharabi, R. M.
and
Al-Abbas, H. S.
2017.
Truncation error estimates for generalized Hermite sampling.
Numerical Algorithms,
Vol. 74,
Issue. 2,
p.
481.
Annaby, M. H.
and
Asharabi, R. M.
2018.
Sinc-interpolants in the energy plane for regular solution, Jost function, and its zeros of quantum scattering.
Journal of Mathematical Physics,
Vol. 59,
Issue. 1,
Annaby, M. H.
Asharabi, R. M.
and
Tharwat, M. M.
2021.
New Sinc Methods of Numerical Analysis.
p.
255.

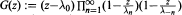 where {
where {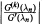 is bounded by a constant independent of
is bounded by a constant independent of 