Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cao, Xiaodong
and
Zhang, Qi S.
2011.
The conjugate heat equation and Ancient solutions of the Ricci flow.
Advances in Mathematics,
Vol. 228,
Issue. 5,
p.
2891.
Zhang, Qi S.
2012.
Extremal of Log Sobolev inequality and W entropy on noncompact manifolds.
Journal of Functional Analysis,
Vol. 263,
Issue. 7,
p.
2051.
Wu, Jia-Yong
2012.
Differential Harnack inequalities for nonlinear heat equations with potentials under the Ricci flow.
Pacific Journal of Mathematics,
Vol. 257,
Issue. 1,
p.
199.
Yu, Chengjie
2012.
Some estimates of fundamental solutions on noncompact manifolds with time-dependent metrics.
Manuscripta Mathematica,
Vol. 139,
Issue. 3-4,
p.
321.
Wu, Jia-Yong
2012.
Interpolating between constrained Li–Yau and Chow–Hamilton Harnack inequalities for a nonlinear parabolic equation.
Journal of Mathematical Analysis and Applications,
Vol. 396,
Issue. 1,
p.
363.
Simon, Miles
2013.
Local smoothing results for the Ricci flow in dimensions two and three.
Geometry & Topology,
Vol. 17,
Issue. 4,
p.
2263.
Zhu, Anqiang
2013.
Differential Harnack inequalities for the backward heat equation with potential under the harmonic–Ricci flow.
Journal of Mathematical Analysis and Applications,
Vol. 406,
Issue. 2,
p.
502.
Hsu, Shu-Yu
2014.
Some results for the Perelman LYH-type inequality.
Discrete & Continuous Dynamical Systems - A,
Vol. 34,
Issue. 9,
p.
3535.
Ma, Bingqing
and
Li, Jing
2014.
Gradient estimates of porous medium equations under the Ricci flow.
Journal of Geometry,
Vol. 105,
Issue. 2,
p.
313.
Zhu, Meng
2015.
Davies type estimate and the heat kernel bound under the Ricci flow.
Transactions of the American Mathematical Society,
Vol. 368,
Issue. 3,
p.
1663.
Deruelle, Alix
2016.
Smoothing out positively curved metric cones by Ricci expanders.
Geometric and Functional Analysis,
Vol. 26,
Issue. 1,
p.
188.
Xu, Guoyi
2017.
An equation linking 𝒲-entropy with reduced volume.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2017,
Issue. 727,
p.
49.
Thac Dung, Nguyen
2017.
Hamilton type gradient estimate for a nonlinear diffusion equation on smooth metric measure spaces.
Differential Geometry and its Applications,
Vol. 51,
Issue. ,
p.
153.
Liu, Xian-Gao
and
Wang, Kui
2017.
A Gaussian upper bound of the conjugate heat equation along Ricci-harmonic flow.
Pacific Journal of Mathematics,
Vol. 287,
Issue. 2,
p.
465.
Li, Yu
2018.
Ricci flow on asymptotically Euclidean manifolds.
Geometry & Topology,
Vol. 22,
Issue. 3,
p.
1837.
Li, Yu
and
Wang, Bing
2020.
Heat kernel on Ricci shrinkers.
Calculus of Variations and Partial Differential Equations,
Vol. 59,
Issue. 6,
Huang, Hongzhi
Kong, Lingling
Rong, Xiaochun
and
Xu, Shicheng
2020.
Collapsed manifolds with Ricci bounded covering geometry.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 11,
p.
8039.
Di Giovanni, Francesco
2020.
Ricci flow of warped Berger metrics on $${\mathbb {R}}^{4}$$.
Calculus of Variations and Partial Differential Equations,
Vol. 59,
Issue. 5,
Zhang, Yongjia
2020.
On the equivalence between noncollapsing and bounded entropy for ancient solutions to the Ricci flow.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2020,
Issue. 762,
p.
35.
Wu, Jiayong
2020.
New Differential Harnack Inequalities for Nonlinear Heat Equations.
Chinese Annals of Mathematics, Series B,
Vol. 41,
Issue. 2,
p.
267.
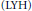 $\left( \text{LHY} \right)$ type inequality for fundamental solutions of the conjugate heat equation corresponding to the Ricci flow on compact manifolds. As an application of the
$\left( \text{LHY} \right)$ type inequality for fundamental solutions of the conjugate heat equation corresponding to the Ricci flow on compact manifolds. As an application of the 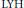 $\text{LHY}$ inequality, Perelman proved a pseudolocality result for the Ricci flow on compact manifolds. In this article we provide the details for the proofs of these results in the case of a complete noncompact Riemannian manifold. Using these results we prove that under certain conditions, a finite time singularity of the Ricci flow must form within a compact set. The conditions are satisfied by asymptotically flatmanifolds. We also prove a long time existence result for the Kähler-Ricci flow on complete nonnegatively curved Kähler manifolds.
$\text{LHY}$ inequality, Perelman proved a pseudolocality result for the Ricci flow on compact manifolds. In this article we provide the details for the proofs of these results in the case of a complete noncompact Riemannian manifold. Using these results we prove that under certain conditions, a finite time singularity of the Ricci flow must form within a compact set. The conditions are satisfied by asymptotically flatmanifolds. We also prove a long time existence result for the Kähler-Ricci flow on complete nonnegatively curved Kähler manifolds.
