Article contents
Power Residues of Fourier Coefficients of Modular Forms
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 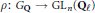 $\rho :\,{{G}_{Q}}\,\to \,\text{G}{{\text{L}}_{n}}\left( {{Q}_{\ell }} \right)$ be a motivic
$\rho :\,{{G}_{Q}}\,\to \,\text{G}{{\text{L}}_{n}}\left( {{Q}_{\ell }} \right)$ be a motivic  $\ell $ -adic Galois representation. For fixed
$\ell $ -adic Galois representation. For fixed 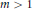 $m\,>\,1$ we initiate an investigation of the density of the set of primes
$m\,>\,1$ we initiate an investigation of the density of the set of primes 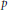 $p$ such that the trace of the image of an arithmetic Frobenius at
$p$ such that the trace of the image of an arithmetic Frobenius at 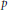 $p$ under
$p$ under  $\rho $ is an
$\rho $ is an 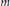 $m$ -th power residue modulo
$m$ -th power residue modulo 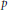 $p$ . Based on numerical investigations with modular forms we conjecture (with Ramakrishna) that this density equals
$p$ . Based on numerical investigations with modular forms we conjecture (with Ramakrishna) that this density equals 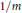 $1/m$ whenever the image of
$1/m$ whenever the image of  $\rho $ is open. We further conjecture that for such
$\rho $ is open. We further conjecture that for such  $\rho $ the set of these primes
$\rho $ the set of these primes 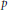 $p$ is independent of any set defined by Cebatorev-style Galois-theoretic conditions (in an appropriate sense). We then compute these densities for certain
$p$ is independent of any set defined by Cebatorev-style Galois-theoretic conditions (in an appropriate sense). We then compute these densities for certain 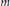 $m$ in the complementary case of modular forms of
$m$ in the complementary case of modular forms of 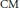 $\text{CM}$ -type with rational Fourier coefficients; our proofs are a combination of the Cebatorev density theorem (which does apply in the
$\text{CM}$ -type with rational Fourier coefficients; our proofs are a combination of the Cebatorev density theorem (which does apply in the 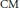 $\text{CM}$ case) and reciprocity laws applied to Hecke characters. We also discuss a potential application (suggested by Ramakrishna) to computing inertial degrees at
$\text{CM}$ case) and reciprocity laws applied to Hecke characters. We also discuss a potential application (suggested by Ramakrishna) to computing inertial degrees at 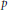 $p$ in abelian extensions of imaginary quadratic fields unramified away from
$p$ in abelian extensions of imaginary quadratic fields unramified away from 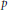 $p$ .
$p$ .
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2005
References
- 3
- Cited by

