Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-10T11:32:02.829Z Has data issue: false hasContentIssue false
  • English
  • Français

Perfect Maps and Epi-Reflective Hulls

Published online by Cambridge University Press:  20 November 2018

Anthony W. Hager
Anthony W. Hager*
Affiliation:
Wesleyan University, Middletown, Connecticut
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

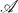The main theorems concern the relation between the - compact spaces and the 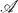-regular spaces, and their analogues in uniform spaces. In either of the categories of Tychonoff spaces or uniform spaces, let 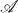be a class of spaces, let 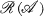be the epi-reflective hull of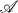 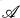se (closed subspaces of products of members of ), let 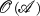be the “onto-reflective” hull of 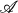(all subspaces of products of members of ), and let r and o be the associated functors. 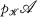Let be the class of spaces which admit a perfect map into a member of . Then, 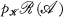is epi-reflective (and in Tych, = 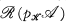but in Unif, the equality fails); call the functor p.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 1 , 01 February 1975 , pp. 11 - 24
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Banaschewski, B., Ûber nulldimensionale Räume, Math. Nach. 13 (1954), 129–140.Google Scholar
2. Blaszczyk, A. and Mioduszewski, J., On factorization of maps through TX, Colloq. Math. 23 (1971), 45–52.Google Scholar
3. Engelking, R. and Mrówka, S. G., E-compact spaces, Bull. Acad. Polon. Sri. Sér. Sci. Math. Astronom. Phys. 6 (1958), 429–436.Google Scholar
4. Franklin, S. P., On epi-reflective hulls, General Topology and Appl. 1 (1971), 29–31.Google Scholar
5. Gillman, L. and Jerison, M., Rings of continuous functions (Van Nostrand Co. Inc., Princeton, 1960).Google Scholar
6. Henriksen, M. and Isbell, J. R., Some properties of compactifications, Duke Math. J. 25 (1958), 83–106.Google Scholar
7. Herrlich, H., Topologische Reflexionen und Coreflexionen, Springer-Verlag Lecture Notes 78, Berlin, 1968.Google Scholar
8. Herrlich, H., Categorical topology, General Topology and Appl. 1 (1971), 1–15.Google Scholar
9. Herrlich, H., A generalization of perfect maps, Proc. Third Prague Symposium on General Topology (1971), 187–191; Academia, Prague, 1972.Google Scholar
10. Herrlich, H. and van der Slot, J., Properties which are closely related to compactness, Proc. Kon. Nederl. Akad. V. Weten 70 (1967), 524–529.Google Scholar
11. Isbell, J. R., Uniform neighborhood retracts, Pacific J. Math. 11 (1961), 609–648.Google Scholar
12. Isbell, J. R., Uniform spaces (Amer. Math. Soc, Providence, 1964).Google Scholar
13. Kennison, J., Reflective functors in general topology and elsewhere, Trans. Amer. Math. Soc. 118 (1965), 303–315.Google Scholar
14. Nyikos, P., (a) Not every O-dimensional realcompact space is N-compact, Bull. Amer. Math. Soc. 77 (1971), 392–396. (b) Prabir Roy's space A is not N-compact, General Topology and Appl. 3 (1973), 197–210.Google Scholar
15. Rice, M. D., Covering and function theoretic properties of uniform spaces, (Ph.D. Thesis, Wesleyan University, 1973).Google Scholar
16. Tsai, J. H., On E-compact spaces and generalizations of perfect maps (to appear).Google Scholar
17. Zener, P., Certain subsets of metacompact spaces and subparacompact spaces are realcompact, Can. J. Math. 24 (1972), 825–829.Google Scholar