Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Candan, T.
and
Dahiya, R.S.
2004.
Oscillation behavior of nth order neutral differential equations with continuous delay.
Journal of Mathematical Analysis and Applications,
Vol. 290,
Issue. 1,
p.
105.
Dahiya, R. S.
and
Zafer, A.
2007.
Oscillation of Higher-Order Neutral-Type Periodic Differential Equations with Distributed Arguments.
Journal of Inequalities and Applications,
Vol. 2007,
Issue. ,
p.
1.
Berezansky, Leonid
and
Braverman, Elena
2008.
Linearized oscillation theory for a nonlinear equation with a distributed delay.
Mathematical and Computer Modelling,
Vol. 48,
Issue. 1-2,
p.
287.
Agarwal, Ravi P.
Berezansky, Leonid
Braverman, Elena
and
Domoshnitsky, Alexander
2012.
Nonoscillation Theory of Functional Differential Equations with Applications.
p.
171.
Agarwal, Ravi P.
Berezansky, Leonid
Braverman, Elena
and
Domoshnitsky, Alexander
2012.
Nonoscillation Theory of Functional Differential Equations with Applications.
p.
149.

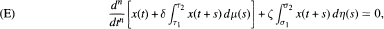
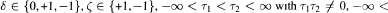 σ1 < σ 2 < ∞ and
σ1 < σ 2 < ∞ and