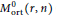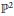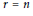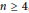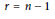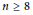Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jardim, Marcos
Marchesi, Simone
and
Wissdorf, Anna
2016.
Moduli of autodual instanton bundles.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 47,
Issue. 3,
p.
823.
Franco, Emilio
Jardim, Marcos
and
Marchesi, Simone
2017.
Branes in the moduli space of framed sheaves.
Bulletin des Sciences Mathématiques,
Vol. 141,
Issue. 4,
p.
353.
Andrade, Aline V.
Marchesi, Simone
and
Miró-Roig, Rosa M.
2020.
Irreducibility of the moduli space of orthogonal instanton bundles on $$\mathbb {P}^n$$.
Revista Matemática Complutense,
Vol. 33,
Issue. 1,
p.
271.
Franco, Emilio
2023.
Deformation theory of orthogonal and symplectic sheaves.
Journal of Geometry and Physics,
Vol. 189,
Issue. ,
p.
104834.