Article contents
Orbital Integrals on p-Adic Lie Algebras
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $G$ be a connected reductive
$G$ be a connected reductive 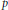 $p$ -adic group and let
$p$ -adic group and let 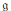 $\mathfrak{g}$ be its Lie algebra. Let
$\mathfrak{g}$ be its Lie algebra. Let 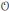 $\mathcal{O}$ be any
$\mathcal{O}$ be any  $G$ -orbit in
$G$ -orbit in 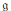 $\mathfrak{g}$ . Then the orbital integral
$\mathfrak{g}$ . Then the orbital integral 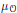 ${{\mu }_{\mathcal{O}}}$ corresponding to
${{\mu }_{\mathcal{O}}}$ corresponding to 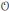 $\mathcal{O}$ is an invariant distribution on
$\mathcal{O}$ is an invariant distribution on 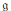 $\mathfrak{g}$ , and Harish-Chandra proved that its Fourier transform
$\mathfrak{g}$ , and Harish-Chandra proved that its Fourier transform  ${{\hat{\mu }}_{\mathcal{O}}}$ is a locally constant function on the set
${{\hat{\mu }}_{\mathcal{O}}}$ is a locally constant function on the set 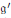 ${\mathfrak{g}}'$ of regular semisimple elements of
${\mathfrak{g}}'$ of regular semisimple elements of 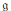 $\mathfrak{g}$ . If
$\mathfrak{g}$ . If 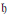 $\mathfrak{h}$ is a Cartan subalgebra of
$\mathfrak{h}$ is a Cartan subalgebra of 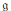 $\mathfrak{g}$ , and
$\mathfrak{g}$ , and 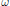 $\omega $ is a compact subset of
$\omega $ is a compact subset of 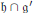 $\mathfrak{h}\,\cap \,{\mathfrak{g}}'$ , we give a formula for
$\mathfrak{h}\,\cap \,{\mathfrak{g}}'$ , we give a formula for 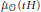 ${{\hat{\mu }}_{\mathcal{O}}}\left( tH \right)$ for
${{\hat{\mu }}_{\mathcal{O}}}\left( tH \right)$ for 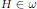 $H\,\in \,\omega $ and
$H\,\in \,\omega $ and 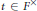 $t\,\in \,{{F}^{\times }}$ sufficiently large. In the case that
$t\,\in \,{{F}^{\times }}$ sufficiently large. In the case that 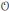 $\mathcal{O}$ is a regular semisimple orbit, the formula is already known by work of Waldspurger. In the case that
$\mathcal{O}$ is a regular semisimple orbit, the formula is already known by work of Waldspurger. In the case that 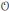 $\mathcal{O}$ is a nilpotent orbit, the behavior of
$\mathcal{O}$ is a nilpotent orbit, the behavior of  ${{\hat{\mu }}_{\mathcal{O}}}$ at infinity is already known because of its homogeneity properties. The general case combines aspects of these two extreme cases. The formula for
${{\hat{\mu }}_{\mathcal{O}}}$ at infinity is already known because of its homogeneity properties. The general case combines aspects of these two extreme cases. The formula for  ${{\hat{\mu }}_{\mathcal{O}}}$ at infinity can be used to formulate a “theory of the constant term” for the space of distributions spanned by the Fourier transforms of orbital integrals. It can also be used to show that the Fourier transforms of orbital integrals are “linearly independent at infinity.”
${{\hat{\mu }}_{\mathcal{O}}}$ at infinity can be used to formulate a “theory of the constant term” for the space of distributions spanned by the Fourier transforms of orbital integrals. It can also be used to show that the Fourier transforms of orbital integrals are “linearly independent at infinity.”
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2000
References
- 1
- Cited by

