Hostname: page-component-cb9f654ff-hn9fh Total loading time: 0 Render date: 2025-08-30T18:40:47.408Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Vanishing of μ-Invariants of Elliptic Curves over ℚ

Published online by Cambridge University Press:  20 November 2018

Mak Trifković
Mak Trifković*
Affiliation:
Department of Mathematics, McGill University, Montreal, QC, H3A 2T5, e-mail: mak@math.mcgill.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

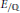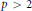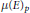Let ${{E}_{/\mathbb{Q}}}$ be an elliptic curve with good ordinary reduction at a prime $p\,>\,2$ . It has a welldefined Iwasawa $\mu $ -invariant $\mu {{\left( E \right)}_{p}}$ which encodes part of the information about the growth of the Selmer group 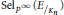$\text{Se}{{\text{l}}_{{{p}^{\infty }}}}\left( {{E}_{/{{K}_{n}}}} \right)$ as 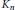${{K}_{n}}$ ranges over the subfields of the cyclotomic 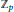${{\mathbb{Z}}_{p}}$ -extension 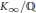${{K}_{\infty }}/\mathbb{Q}$ . Ralph Greenberg has conjectured that any such $E$ is isogenous to a curve 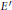${E}'$ with 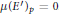$\mu {{\left( {{E}'} \right)}_{p}}\,=\,0$ . 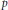In this paper we prove Greenberg's conjecture for infinitely many curves $E$ with a rational $p$ -torsion point, 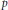$p$ = 3 or 5, no two of our examples having isomorphic 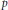$p$ -torsion. The core of our strategy is a partial explicit evaluation of the global duality pairing for finite flat group schemes over rings of integers.

Keywords

11R23

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 4 , 01 August 2005 , pp. 812 - 843
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Cremona, J. E., Algorithms for Modular Elliptic Curves. Second edition. Cambridge University Press, Cambridge, 1997.Google Scholar
[2] Drinen, M. J., Finite submodules and Iwasawa μ-invariants. J. Number Theory 93(2002), 1–22.Google Scholar
[3] Greenberg, R., Iwasawa theory for elliptic curves. In: Arithmetic Theory of Elliptic Curves, Lecture Notes in Math. 1716, Springer, Berlin, 1999, pp. 51–144.Google Scholar
[4] Greenberg, R. and Vatsal, V., On the Iwasawa invariants of elliptic curves. Invent.Math. 142(2000), 17–63.Google Scholar
[5] Kubert, D. S., Universal bounds on the torsion of elliptic curves. Proc. LondonMath. Soc. (3) 33(1976), 193–237.Google Scholar
[6] Mazur, B., Rational points of abelian varieties with values in towers of number fields. Invent.Math. 18(1972), 183–266.Google Scholar
[7] Milne, J. S., Étale Cohomology. PrincetonMathematical Series 33, Princeton University Press, Princeton, NJ, 1980.Google Scholar
[8] Perrin-Riou, B., Variation de la fonction L p-adique par isogénie. In: Algebraic Number Theory, Adv. Stud. Pure Math. 17, Academic Press, Boston, MA, 1989, pp. 347–358.Google Scholar
[9] Rubin, K., Euler systems and modular elliptic curves. In: Galois Representations in Arithmetic Algebraic Geometry, (Scholl, A. and Taylor, R., eds.), LondonMath. Soc. Lecture Note Ser. 254, Cambridge University Press, Cambridge, 1998, pp. 351–367.Google Scholar
[10] Schneider, P., The μ invariant of isogenies. J. IndianMath. Soc. (N.S.) 52(1988), 159–170.Google Scholar
[11] Vatsal, V., Special values of anticyclotomic L-functions. Duke Math. J. 116(2003), 219–261.Google Scholar
[12] Vatsal, V., Multiplicative-type subgroups of J0(N) and applications to elliptic curves, to appear in J. Inst.Math. Jussieu.Google Scholar