Hostname: page-component-cb9f654ff-rkzlw Total loading time: 0 Render date: 2025-08-28T23:59:23.187Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Uniqueness of the Coefficient Ring in a Group Ring

Published online by Cambridge University Press:  20 November 2018

Isabelle Adjaero  and
Eugene Spiegel
Isabelle Adjaero
Affiliation:
University of Nigeria – Nsukka, Ahambra State, Nigeria
Eugene Spiegel
Affiliation:
University of Connecticut, Storrs, Connecticut
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R 1 and R 2 be commutative rings with identities, G a group and R 1 G and R 2 G the group ring of G over R 1 and R 2 respectively. The problem that motivates this work is to determine what relations exist between R 1 and R 2 if R 1 G and R 2 G are isomorphic. For example, is the coefficient ring R 1 an invariant of R 1 G? This is not true in general as the following example shows. Let H be a group and

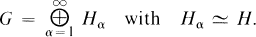
If R 1 is a commutative ring with identity and R 2 = R 1 H, then

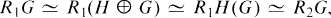
but R 1 needn't be isomorphic to R 2.

Several authors have investigated the problem when G = <x>, the infinite cyclic group, partly because of its closeness to R[x], the ring of polynomials over R.

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 4 , 01 August 1983 , pp. 654 - 673
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Adjaero, I., Uniqueness of the coefficient ring and related problems in group rings, (PH.D. Thesis) University of Connecticut (1980).Google Scholar
2. Akasaki, T., ldempotent ideals in integral group rings, J. Algebra 23 (1972), 343–346.Google Scholar
3. Batman, J. M. and Coleman, D. B., Group algebras with nilpotent unit groups, Proc. Amer. Math. Soc. 79 (1968). 448–449.Google Scholar
4. Burgess, W. D., On semi-perfect group rings. Can. Math. Bull. 12 (1969), 645–652.Google Scholar
5. Cliff, G. H. and Sehgal, S. K., On the trace of an idempotent in a group ring, Proc. Amer. Math. Soc. 62 (1977), 11–14.Google Scholar
6. Coleman, D. B., Finite groups with isomorphic group algebras. Trans. Amer. Math. Soc. 105 (1962), 1–8.Google Scholar
7. Coleman, D. B., On group rings. Can. J. Math. 22 (1970), 249–254.Google Scholar
8. Connell, I. G., On the group ring, Can. J. Math. 75 (1963), 650–685.Google Scholar
9. Formanek, E., Idempofents in Noetherian group rings, Can. J. Math. 25 (1973). 366–369.Google Scholar
10. Grunenfelder, L. and Parmenter, M. M., Isomorphic group rings with non-isomorphic coefficient rings. Can. Math. Bull, (to appear).CrossRefGoogle Scholar
11. Hampton, C. R. and Passman, D. S., On the semisimplicity of group rings of solvable groups. Transactions of the Amer. Math. Soc. 173 (1972), 289–300.Google Scholar
12. Higman, G., The units of group rings, Proc. London Math. J. 46 (1940), 231–248.Google Scholar
13. Hochester, M., Non-uniqueness of coefficient rings in a polynomial ring, Proc. Amer. Math. Soc. 34 (1912), 81–82.Google Scholar
14. Hungerford, W. T., Algebra (Holt Rinehart and Winston, 1974).Google Scholar
15. Lantz, D. C., R-automorphisms of RG for G abelian torsion free, Proc. amer. Math. Soc. 61 (1976), 1–6.Google Scholar
16. May, W., Group algebras over finitely generated rings, J. of Alg. 39 (1976), 483–511.Google Scholar
17. May, W., Isomorphism of group algebras, J. of Alg. 40 (1976), 10–18.Google Scholar
18. Parmenter, M. M., Isomorphic group rings, Can. Math. Bull. 18 (1975), 567–576.Google Scholar
19. Parmenter, M. M., Coefficient rings of isomorphic group rings. Bol. Soc. Bras. Mat. 7 (1976), 59–63.Google Scholar
20. Parmenter, M. M. and Sehgal, S. K., Uniqueness of the coefficient ting in some group rings. Can. Math. Bull. 76 (1973), 551–555.Google Scholar
21. Passman, D. S., Nil ideals in group rings, Mich. Math. J. 9 (1962), 375–384.Google Scholar
22. Passman, D. S., Radicals of group rings, Comm. in Alg. 2 (1974), 295–305.Google Scholar
23. Passman, D. S., The algebraic structure of group rings (John Wiley & Sons, New York, 1977).Google Scholar
24. Rudin, W. and Schneider, H., Idempotents in group rings, Duke Math. J. 31 (1964), 585–602.Google Scholar
25. Sehgal, S. K., Topics in group rings (Marcel Dekker, Inc., New York & Basel, 1978).Google Scholar
26. Sehgal, S. K., Units in commutative integral group rings. Math. J. Okayama Univ. 14 (1970), 135–138.Google Scholar