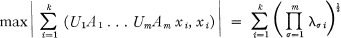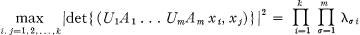Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mirsky, L.
1958.
Maximum Principles in matrix theory.
Proceedings of the Glasgow Mathematical Association,
Vol. 4,
Issue. 1,
p.
34.
Marcus, Marvin
1960.
Some Properties and Applications of Doubly Stochastic Matrices.
The American Mathematical Monthly,
Vol. 67,
Issue. 3,
p.
215.
Capel, H.W
and
Tindemans, P.A.J
1974.
An inequality for the trace of matrix products.
Reports on Mathematical Physics,
Vol. 6,
Issue. 2,
p.
225.
Tindemans, P.A.J.
and
Capel, H.W.
1975.
On the free energy in systems with separable interactions. III.
Physica A: Statistical Mechanics and its Applications,
Vol. 79,
Issue. 5,
p.
478.
Mirsky, L.
1975.
A trace inequality of John von Neumann.
Monatshefte für Mathematik,
Vol. 79,
Issue. 4,
p.
303.
Grone, Robert
and
Marcus, Marvin
1977.
Isometries of matrix algebras.
Journal of Algebra,
Vol. 47,
Issue. 1,
p.
180.
1979.
Inequalities - Theory of Majorization and Its Applications.
Vol. 143,
Issue. ,
p.
531.
Marcus, Marvin
and
Sandy, Markus
1982.
Three elementary proofs of the goldberg-straus theorem on numerical radii.
Linear and Multilinear Algebra,
Vol. 11,
Issue. 3,
p.
243.
Simon, Barry
1983.
Nonclassical eigenvalue asymptotics.
Journal of Functional Analysis,
Vol. 53,
Issue. 1,
p.
84.
Tam, Tin-Yau
1984.
A unified extension of some results of Thompson, Marcus and Moyls.
Monatshefte für Mathematik,
Vol. 98,
Issue. 2,
p.
157.
Miranda, H.
and
Thompson, Robert C.
1993.
A trace inequality with a subtracted term.
Linear Algebra and its Applications,
Vol. 185,
Issue. ,
p.
165.
Grone, Robert
1994.
A biography of Marvin Marcus.
Linear Algebra and its Applications,
Vol. 201,
Issue. ,
p.
1.

 . For
. For 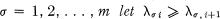 be the characteristic roots of A
be the characteristic roots of A