In a 1987 paper, Gross introduced certain curves associated to a definite quaternion algebra $B$ over 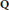$\mathbf{Q}$ ; he then proved an analog of his result with Zagier for these curves. In Gross’ paper, the curves were defined in a somewhat ad hoc manner. In this article, we present an interpretation of these curves as projective varieties arising from graded rings of automorphic forms on 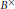${{B}^{\times }}$ , analogously to the construction in the Satake compactification. To define such graded rings, one needs to introduce a “multiplication” of automorphic forms that arises from the representation ring of 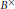${{B}^{\times }}$ . The resulting curves are unions of projective lines equipped with a collection of Hecke correspondences. They parametrize two-dimensional complex tori with quaternionic multiplication. In general, these complex tori are not abelian varieties; they are algebraic precisely when they correspond to 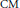$\text{CM}$ points on these curves, and are thus isogenous to a product 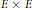$E\,\times \,E$ , where $E$ is an elliptic curve with complex multiplication. For these 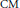$\text{CM}$ points one can make a relation between the action of the 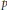$p$ -th Hecke operator and Frobenius at 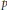$p$ , similar to the well-known congruence relation of Eichler and Shimura.