Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Willenbring, Jeb F
2001.
A Stable Range for Dimensions of Homogeneous O(n)-Invariant Polynomials on the n×n Matrices.
Journal of Algebra,
Vol. 242,
Issue. 2,
p.
691.
Willenbring, Jeb
2002.
An application of the Littlewood restriction formula to the Kostant-Rallis Theorem.
Transactions of the American Mathematical Society,
Vol. 354,
Issue. 11,
p.
4393.
Howe, Roger
Tan, Eng-Chye
and
Willenbring, Jeb F.
2008.
The Stability of Graded Multiplicity in the Setting of the Kostant-Rallis Theorem.
Transformation Groups,
Vol. 13,
Issue. 3-4,
p.
617.
Ž. Đoković, Dragomir
2009.
On orthogonal and special orthogonal invariants of a single matrix of small order.
Linear and Multilinear Algebra,
Vol. 57,
Issue. 4,
p.
345.
Garsia, A.
Wallach, N.
Xin, G.
and
Zabrocki, M.
2009.
Hilbert series of invariants, constant terms and Kostka–Foulkes polynomials.
Discrete Mathematics,
Vol. 309,
Issue. 16,
p.
5206.
Panyushev, Dmitri I.
2010.
Generalised Kostka–Foulkes polynomials and cohomology of line bundles on homogeneous vector bundles.
Selecta Mathematica,
Vol. 16,
Issue. 2,
p.
315.
Kraft, Hanspeter
and
Wallach, Nolan R.
2010.
Symmetry and Spaces.
Vol. 278,
Issue. ,
p.
153.
van Groningen, Anthony
and
Willenbring, Jeb F.
2014.
Developments and Retrospectives in Lie Theory.
Vol. 38,
Issue. ,
p.
385.
Harris, Pamela E.
and
Willenbring, Jeb F.
2014.
Symmetry: Representation Theory and Its Applications.
Vol. 257,
Issue. ,
p.
305.
Frohmader, Andrew
and
Heaton, Alexander
2025.
Stable graded multiplicities for harmonics on a cyclic quiver.
Algebraic Combinatorics,
Vol. 7,
Issue. 6,
p.
1603.
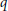 $q$-Analogs of a Theorem of Kostant-Rallis
$q$-Analogs of a Theorem of Kostant-Rallis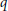 $q$-analog of Kostant’smultiplicity formula for the action of a semisimple Lie group on the polynomials on its Lie algebra are given in the context of the Kostant-Rallis theorem. They correspond to the cases of real semisimple Lie groups with one conjugacy class of Cartan subgroup. In the second part of the paper a
$q$-analog of Kostant’smultiplicity formula for the action of a semisimple Lie group on the polynomials on its Lie algebra are given in the context of the Kostant-Rallis theorem. They correspond to the cases of real semisimple Lie groups with one conjugacy class of Cartan subgroup. In the second part of the paper a 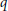 $q$-analog of the Kostant-Rallis theorem is given for the real group
$q$-analog of the Kostant-Rallis theorem is given for the real group 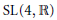 $\text{SL(4,}\,\mathbb{R}\text{)}$ (that is
$\text{SL(4,}\,\mathbb{R}\text{)}$ (that is 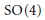 $\text{SO}(4)$ acting on symmetric 4 × 4 matrices). This example plays two roles. First it contrasts with the examples of the first part. Second it has implications to the study of entanglement of mixed 2 qubit states in quantum computation.
$\text{SO}(4)$ acting on symmetric 4 × 4 matrices). This example plays two roles. First it contrasts with the examples of the first part. Second it has implications to the study of entanglement of mixed 2 qubit states in quantum computation.