Article contents
On Some Generalized Rapoport–Zink Spaces
Published online by Cambridge University Press: 03 May 2019
Abstract
We enlarge the class of Rapoport–Zink spaces of Hodge type by modifying the centers of the associated 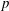 $p$-adic reductive groups. Such obtained Rapoport–Zink spaces are said to be of abelian type. The class of Rapoport–Zink spaces of abelian type is strictly larger than the class of Rapoport–Zink spaces of Hodge type, but the two type spaces are closely related as having isomorphic connected components. The rigid analytic generic fibers of Rapoport–Zink spaces of abelian type can be viewed as moduli spaces of local
$p$-adic reductive groups. Such obtained Rapoport–Zink spaces are said to be of abelian type. The class of Rapoport–Zink spaces of abelian type is strictly larger than the class of Rapoport–Zink spaces of Hodge type, but the two type spaces are closely related as having isomorphic connected components. The rigid analytic generic fibers of Rapoport–Zink spaces of abelian type can be viewed as moduli spaces of local 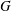 $G$-shtukas in mixed characteristic in the sense of Scholze.
$G$-shtukas in mixed characteristic in the sense of Scholze.
We prove that Shimura varieties of abelian type can be uniformized by the associated Rapoport–Zink spaces of abelian type. We construct and study the Ekedahl–Oort stratifications for the special fibers of Rapoport–Zink spaces of abelian type. As an application, we deduce a Rapoport–Zink type uniformization for the supersingular locus of the moduli space of polarized K3 surfaces in mixed characteristic. Moreover, we show that the Artin invariants of supersingular K3 surfaces are related to some purely local invariants.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
This work was partially supported by the Chinese Academy of Sciences grants 50Y64198900, 29Y64200900, the Recruitment Program of Global Experts of China, and the NSFC grants No. 11631009 and No. 11688101.
References
- 9
- Cited by


