Hostname: page-component-7f64f4797f-zzvtc Total loading time: 0 Render date: 2025-11-03T23:23:30.764Z Has data issue: false hasContentIssue false
  • English
  • Français

On p-Adic Properties of Central L-Values of Quadratic Twists of an Elliptic Curve

Published online by Cambridge University Press:  20 November 2018

Kartik Prasanna
Kartik Prasanna*
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI, USA, e-mail: kartik.prasanna@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

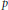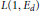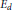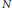We study $p$ -indivisibility of the central values $L\left( 1,\,{{E}_{d}} \right)$ of quadratic twists ${{E}_{d}}$ of a semi-stable elliptic curve $E$ of conductor $N$ . A consideration of the conjecture of Birch and Swinnerton-Dyer shows that the set of quadratic discriminants $d$ splits naturally into several families 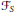${{\mathcal{F}}_{S}}$ , indexed by subsets $S$ of the primes dividing 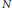$N$ . Let 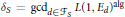${{\delta }_{S}}={{\gcd }_{d\in {{\mathcal{F}}_{S}}}}L{{(1,{{E}_{d}})}^{\text{alg}}}$ , where 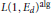$L{{(1,{{E}_{d}})}^{\text{alg}}}$ denotes the algebraic part of the central $L$ -value, 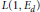$L(1,\,{{E}_{d}})$ . Our main theorem relates the 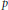$p$ -adic valuations of 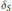${{\delta }_{S}}$ as $S$ varies. As a consequence we present an application to a refined version of a question of Kolyvagin. Finally we explain an intriguing (albeit speculative) relation between Waldspurger packets on 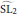$\widetilde{\text{S}{{\text{L}}_{2}}}$ and congruences of modular forms of integral and half-integral weight. In this context, we formulate a conjecture on congruences of half-integral weight forms and explain its relevance to the problem of 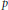$p$ -indivisibility of $L$ -values of quadratic twists.

Keywords

11G4011F6711G05

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 2 , 01 April 2010 , pp. 400 - 414
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Abbes, A. and Ullmo, E., À propos de la conjecture de Manin pour les courbes elliptiques modulaires. Compositio Math. 103(1996), no. 3, 269–286.Google Scholar
[2] Baruch, E. M. and Mao, Z., Central value of automorphic L-functions. Geom. Funct. Anal. 17(2007), no. 2, 333–384. doi:10.1007/s00039-007-0601-3Google Scholar
[3] Kato, K., p-adic Hodge theory and values of zeta functions of modular forms. Cohomologies p-adiques et applications arithmétiques. III. Astérisque No. 295 (2004), 117–290.Google Scholar
[4] Kohnen, W., Newforms of half-integral weight. J. Reine Angew. Math. 333(1982), 32–72.Google Scholar
[5] Kohnen, W. and Ono, K., Indivisibility of class numbers of imaginary quadratic fields and orders of Tate-Shafarevich groups of elliptic curves with complex multiplication. Invent. Math. 135(1999), no. 2, 387–398. doi:10.1007/s002220050290Google Scholar
[6] Michel, P., The subconvexity problem for Rankin-Selberg L-functions and equidistribution of Heegner points. Ann. of Math. 160(2004), no. 1, 185–236. doi:10.4007/annals.2004.160.185Google Scholar
[7] Ono, K. and Skinner, C., Fourier coefficients of half-integral weight modular forms modulo l. Ann. of Math. 147(1998), no. 2, 453–470. doi:10.2307/121015Google Scholar
[8] Prasanna, K., Integrality of a ratio of Petersson norms and level-lowering congruences. Ann. of Math. 163(2006), no. 3, 901–967. doi:10.4007/annals.2006.163.901Google Scholar
[9] Prasanna, K., Arithmetic properties of the Shimura-Shintani-Waldspurger correspondence.With an appendix by B. Conrad. Invent. Math. 176(2009), no. 3, 521–600. doi:10.1007/s00222-008-0169-zGoogle Scholar
[10] Prasanna, K., On the Fourier coefficients of modular forms of half-integral weight. To appear in Forum. Math.Google Scholar
[11] Ribet, K. A. and Takahashi, S, Parametrizations of elliptic curves by Shimura curves and by classical modular curves. In: Elliptic Curves and Modular Forms. Proc. Nat. Acad. Sci. U.S.A. 94(1997), no. 21, 11110–11114. doi:10.1073/pnas.94.21.11110Google Scholar
[12] Silverman, J. H., The arithmetic of elliptic curves. Corrected reprint of the 1986 original. Graduate Texts in Mathematics 106. Springer-Verlag, New York, 1992.Google Scholar
[13] Shimura, G., On modular forms of half integral weight. Ann. of Math. 97(1973), 440–481. doi:10.2307/1970831Google Scholar
[14] Shimura, G., The critical values of certain zeta functions associated with modular forms of half-integral weight. J. Math. Soc. Japan 33(1981), no. 4, 649–672. doi:10.2969/jmsj/03340649Google Scholar
[15] Takagi, T., The cuspidal class number formula for the modular curves X0(M) with M square-free. J. Algebra 193(1997), no. 1, 180–213. doi:10.1006/jabr.1996.6993Google Scholar
[16] Takahashi, S., Degrees of parametrizations of elliptic curves by Shimura curves. J. Number Theory 90(2001), no. 1, 74–88. doi:10.1006/jnth.2000.2614Google Scholar
[17] Waldspurger, J. L., Correspondance de Shimura. J. Math. Pures Appl. 59(1980), no. 1, 1–132.Google Scholar
[18] Waldspurger, J. L., Sur les coefficients de Fourier des formes modulaires de poids demi-entier. J. Math. Pures Appl. 60(1981), no. 4, 375–484.Google Scholar
[19] Waldspurger, J. L., Correspondances de Shimura et quaternions. Forum Math. 3(1991), no. 3, 219–307. doi:10.1515/form.1991.3.219Google Scholar