Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-24T18:27:38.360Z Has data issue: false hasContentIssue false
  • English
  • Français

On K3 Surface Quotients of K3 or AbelianSurfaces

Published online by Cambridge University Press:  20 November 2018

Alice Garbagnati
Alice Garbagnati*
Affiliation:
Dipartimento di Matematica, Università di Milano, via Saldini 50, I-20133 Milano, Italia e-mail: alice.garbagnati@unimi.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

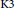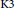The aim of this paper is to prove that a $\text{K3}$ surface is the minimal model of the quotient of an Abelian surface by a group $G$ (respectively of a $\text{K3}$ surface by an Abelian group $G$) if and only if a certain lattice is primitively embedded in its Néron-Severi group. This allows one to describe the coarse moduli space of the 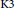$\text{K3}$ surfaces that are (rationally) $G$-covered by Abelian or 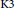$\text{K3}$ surfaces (in the latter case $G$ is an Abelian group). When $G$ has order 2 or $G$ is cyclic and acts on an Abelian surface, this result is already known; we extend it to the other cases.

Moreover, we prove that a 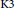$\text{K3}$ surface 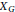${{X}_{G}}$ is the minimal model of the quotient of an Abelian surface by a group $G$ if and only if a certain configuration of rational curves is present on 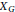${{X}_{G}}$. Again, this result was known only in some special cases, in particular, if $G$ has order 2 or 3.

Keywords

14J2814J5014J10K3 surfacesKummer surfacesKummer type latticequotient surfaces
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 2 , 01 April 2017 , pp. 338 - 372
Copyright
Copyright © Canadian Mathematical Society 2017

References

[Bal] Barth, W., K3 surfaces with nine cusps. Geom. Dedicata 72(1998), no. 2,171–178. http://dx.doi.Org/10.1023/A:1005074306462 Google Scholar
[Ba2] Barth, W., On the classification of K3 surfaces with nine cusps. In: Complex analysis and algebraic geometry, de Gruyter, Berlin, 2000, pp. 41–59.Google Scholar
[Be] Bertin, J., Réseaux de Kummer et surfaces K3. Invent. Math. 93(1988), no. 2, 267–284. http://dx.doi.Org/10.1007/BF01394333 Google Scholar
[BHPV] Barth, W., Hulek, K., Peters, C., and van de Ven, A., Compact complex surfaces. Second edition, Ergebnisse der Mathematik und ihrer Grenzgebiete, 3, A Series of Modern Surveys in Mathematics, Springer-Verlag, Berlin, 2004. http://dx.doi.Org/10.1007/978-3-642-57739-0 Google Scholar
[F] Fujiki, A., Finite automorphism groups of complex tori of dimension two. Publ. Res. Inst. Math. Sci. 24(1988), no. 1, 1–97. http://dx.doi.Org/10.2977/prims/1195175326 Google Scholar
[GS1] Garbagnati, A. and Sarti, A., Projective models ofK3 surfaces with an even set. Adv.Geom. 8(2008), no. 3, 413–440. http://dx.doi.Org/10.1515/ADVCEOM.2008.027 Google Scholar
[GS2] Garbagnati, A., Kummer surfaces and K3 surfaces with (ℤ/2ℤ)44symplectic action. Rocky Mountain J. Math., to appear. arxiv:1305.3514 Google Scholar
[M] Mukai, S., Finite groups of automorphisms of K3 surfaces and the Mathieu group. Invent. Math. 94(1988), no. 1, 183–221. http://dx.doi.org/10.1007/BF01394352 Google Scholar
[MTW] Mongardi, G., Tari, K., and Wandel, M. , Prime order automorphisms of abelian surfaces: a lattice-theoretic point of view. arxiv:1506.05679 Google Scholar
[Nl] Nikulin, V. V., Rummer surfaces. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 39(1975), 278–293; (English) Math. USSR. Izv. 39 (1975/1976), 261–275.Google Scholar
[N2] Nikulin, V. V., Factor groups of groups of the automorphisms of hyperbolic forms with respect to subgroups generated by 2-reflections. Soviet Math. Dokl. 20(1979), 1156–1158.Google Scholar
[N3] Nikulin, V. V.,Finite automorphism groups of Kähler K3 surfaces. Trans. Moscow Math. Soc. 38(1980), 71–135.Google Scholar
[N4] Nikulin, V. V., Integral symmetric bilinear forms and some applications. Math. USSR Izvestija 14(1980), 103–167.Google Scholar
[W] Wendland, K., Consistency of orbifold conformai field theories on K3. Adv. Theor. Math. Phys. 5(2001), no. 3, 429–456.Google Scholar
[X] Xiao, G., Galois covers between K3 surfaces. Ann. Inst. Fourier(Grenoble) 46(1996), no. 1, 73–88. http://dx.doi.Org/10.58O2/aif.1507 Google Scholar