Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Oskolkov, K. I.
1992.
Progress in Approximation Theory.
Vol. 19,
Issue. ,
p.
353.
Yukalov, V.I.
1997.
Local stability of dynamical processes in random media.
Physica A: Statistical Mechanics and its Applications,
Vol. 234,
Issue. 3-4,
p.
725.
Oskolkov, K.
1998.
Schrödinger equation and oscillatory Hilbert transforms of second degree.
The Journal of Fourier Analysis and Applications,
Vol. 4,
Issue. 3,
p.
341.
Oskolkov, K. I.
and
Chakhkiev, M. A.
2010.
On riemann “nondifferentiable” function and Schrödinger equation.
Proceedings of the Steklov Institute of Mathematics,
Vol. 269,
Issue. 1,
p.
186.
Bilyk, Dmitriy
De Carli, Laura
Petukhov, Alexander
Stokolos, Alexander M.
and
Wick, Brett D.
2012.
Recent Advances in Harmonic Analysis and Applications.
Vol. 25,
Issue. ,
p.
3.
Oskolkov, K. I.
and
Chakhkiev, M. A.
2013.
Traces of the discrete Hilbert transform with quadratic phase.
Proceedings of the Steklov Institute of Mathematics,
Vol. 280,
Issue. 1,
p.
248.
Demirci Akarsu, Emek
and
Marklof, Jens
2013.
THE VALUE DISTRIBUTION OF INCOMPLETE GAUSS SUMS.
Mathematika,
Vol. 59,
Issue. 2,
p.
381.
Demirci Akarsu, Emek
2014.
Short incomplete Gauss sums and rational points on metaplectic horocycles.
International Journal of Number Theory,
Vol. 10,
Issue. 06,
p.
1553.
Korolev, M. A.
2015.
On incomplete Gaussian sums.
Proceedings of the Steklov Institute of Mathematics,
Vol. 290,
Issue. 1,
p.
52.
Korolev, M. A.
2017.
On Anatolii Alekseevich Karatsuba’s Works Written in the 1990s and 2000s.
Proceedings of the Steklov Institute of Mathematics,
Vol. 299,
Issue. 1,
p.
1.
Strawn, Nate
2022.
Filament plots for data visualization.
Applied and Computational Harmonic Analysis,
Vol. 60,
Issue. ,
p.
205.
Cellarosi, Francesco
and
Osman, Tariq
2025.
Bounds for smooth theta sums with rational parameters.
Journal of Number Theory,
Vol. 269,
Issue. ,
p.
397.
Demirci Akarsu, Emek
2025.
Finite dimensional distributions for short incomplete Gauss sums.
Journal of Mathematical Analysis and Applications,
Vol. 551,
Issue. 2,
p.
129685.
Kashin, Boris
Stokolos, Alexander
and
Temlyakov, Vladimir
2026.
In Memoriam: Konstantin Il’ich Oskolkov February 17, 1946–August 24, 2024.
Journal of Approximation Theory,
Vol. 313,
Issue. ,
p.
106243.
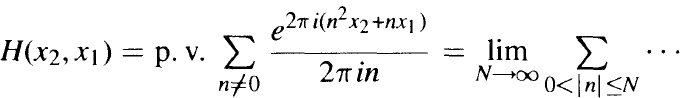 and its connections with the incomplete Gaussian sums
and its connections with the incomplete Gaussian sums 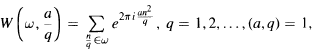 where ω are intervals of length |ω| ≤1. In particular, it is proved that for each fixed x2 and uniformly in X2 the function H(x2, x1 ) is of weakly bounded 2-variation in the variable x1 over the period [0, 1]. In terms of the sums W this means that for collections Ω = {ωk}, consisting of nonoverlapping intervals ωk ∪ [0,1) the following estimate is valid:
where ω are intervals of length |ω| ≤1. In particular, it is proved that for each fixed x2 and uniformly in X2 the function H(x2, x1 ) is of weakly bounded 2-variation in the variable x1 over the period [0, 1]. In terms of the sums W this means that for collections Ω = {ωk}, consisting of nonoverlapping intervals ωk ∪ [0,1) the following estimate is valid: 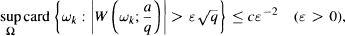 where card denotes the number of elements, and c is an absolute positive constant. The exact value of the best absolute constant к in the estimate
where card denotes the number of elements, and c is an absolute positive constant. The exact value of the best absolute constant к in the estimate 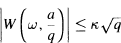 (which is due to G. H. Hardy and J. E. Littlewood) is discussed.
(which is due to G. H. Hardy and J. E. Littlewood) is discussed.
